基本介紹
- 中文名:克利福德代數
- 外文名:Clifford algebra
- 別稱:幾何代數
- 包含:內積和外積
- 提出者:克利福德
- 推廣者:Hestenes
簡介

詳細定義

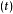
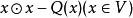
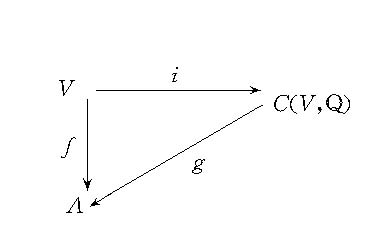
外代數

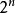


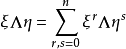

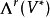


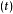
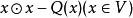


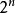


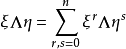

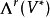
克利福德代數(Clifford algebra),又稱幾何代數(Geometric algebra),綜合了內積和外積兩種運算,是複數代數、四元數代數和外代數的推廣,在幾何和物理中有套用廣泛。...
克利福德(1845~1879)Cliffod,William Kingdo英國數學家。1845年5月4日生於英格蘭埃克塞特,1879年3月3日卒於馬德拉。...
到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展。與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了...
與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了起來.代數溯源 編輯 古希臘數學家丟番圖 如果我們對代數符號不是要求像現在這樣...
威廉·金頓·克利福德(William Kingdon Clifford,1845年5月4日-1879年3月3日),英國數學家兼科學哲學家。他和赫爾曼·格拉斯曼發明了現在稱為幾何代數的範疇。數學...
介紹 克利福德群(Clifford group)克利福德代數乘法群的一個重要子群.若E是特徵為零的域K上的向量空間,CF是CF;的可逆元的乘法群,則是CE的子群,稱為E上的...
與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了起來。 [3] 合成代數對偶空間 編輯 一種特殊的線性空間。即線性空間的線性函式...
與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了起來。循環代數單代數 編輯 單代數又叫單環,是與群論中單群類相對應的基本環...
與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了起來.代數溯源 編輯 古希臘數學家丟番圖 如果我們對代數符號不是要求像現在這樣...
與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了起來。相對自由代數自由代數 編輯 自由代數是具有生成基的一類代數。集合X={x1,...
在表示論這個數學領域中,特殊正交群的旋量表示中,純旋量(pure spinor 或單旋量 simple spinor)是能被克利福德代數的最大可能子空間零化的旋量。它們在1930年代...
每個Cn形成一個巴拿赫代數。G. Bayley Price已寫有關於多重複數的函式論,提供了雙複數系C2的一些性質。多重複數系不能和克利福德代數混淆。因為克利福德代數里-1的...
多重線性代數研究的內容包括:多重線性映射、具有一定對稱性質的多重線性映射、張量空間、張量對稱類、張量代數、對稱張量代數、格拉斯曼代數、外代數、克利福德代數及其...
