基本介紹
- 中文名:有限維向量空間
- 外文名:finite dimensional vector space
- 所屬學科:數學
- 相關概念:線性組合,有限基等
基本介紹
相關概念及定理




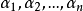
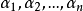







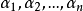
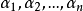


設V是數域P上的一個向量空間,若存在V的有限個向量α1,α2,...,αm使得V的每一個向量均為這m個向量的線性組合,則V稱為數域P上的一個有限維向量空間,...
向量空間中任意一個元素,都可以唯一地表示成基向量的線性組合。如果基中元素個數有限,就稱向量空間為有限維向量空間,將元素的個數稱作向量空間的維數。 [1] ...
[4] 對非零向量空間 V,基是 V 最小的生成集,也是極大線性無關組。如果一個向量空間 V 擁有一個元素個數有限的生成集,那么就稱 V 是一個有限維空間。向量...
若且唯若單位球B = {x:‖x‖≤1}緊湊時,規範向量空間V是局部緊湊的,若且唯若V是有限維的情況下才是這種情況;這是雷斯的引理的結果。 (事實上,更一般的...
因為容易驗證:S 中向量的有限線性組合的集合是包含 S 的一個向量空間,反之任何包含 S 的向量空間必然都包含 S 中向量的有限組合,故兩個定義是等價的。...
如果V 是有限維的那么維數必須為偶數,因為每個奇數階斜對稱矩陣的行列式為 0。非退化斜對稱雙線性形式和非退化“對稱”雙線性形式,比如歐幾里得向量空間的內積,的...
線性變換的主特徵向量是最大特徵值對應的特徵向量。特徵值的幾何重次是相應特徵空間的維數。有限維向量空間上的一個線性變換的譜是其所有特徵值的集合。...
此法變一連續對偶為一線性賦范向量空間,實為巴拿赫空間。對偶空間例子 對任意有限維之 線性賦范向量空間或拓撲向量空間,正如歐幾里得空間,其連續與代數對偶不二。...
紹德爾基(Schauder bases)有限維空間中基概念的一種推廣。線上性代數中,基(也稱為基底)是描述、刻畫向量空間的基本工具。向量空間的基是它的一個特殊的子集,基的...
更為準確地說,定理指出L在K上有一個在有限維向量空間V上的忠實線性表示,使得L與一個V自同態的子代數同構。中文名 Ado定理 外文名 Ado's theorem ...
在有限維向量空間中,也與線性相關與線性變換密切相關,但無需限制於三維組.同時假定有理運算能夠施行(這個極大地影響了計算機科學發展),討論域為任意域,並且要將...
在有限維向量空間中,也與線性相關與線性變換密切相關,但無需限制於三維組。同時假定有理運算能夠施行(極大地影響了計算機科學發展),討論域為任意域,並且要將基本...
給定一個實矩陣A,矩陣AA是A的列向量的格拉姆矩陣,而矩陣AA是A的行向量的格拉姆矩陣。對一般任何域上的有限維向量空間上的雙線性形式B,我們可對一組向量 定義一...
如果基中元素個數有限,就稱向量空間為有限維向量空間,將元素的個數稱作向量空間的維數。同樣的,線性基是一種特殊的基,它通常會在異或運算中出現,它的意義是:...
向量空間分為有限維向量空間與無限維向量空間。在有限維向量空間中,可以找到一組(有限個)向量 ,使得任意一個向量v都可以唯一地表示成這組向量的線性組合:...
向量空間中任意一個元素,都可以唯一地表示成基向量的線性組合。如果基中元素個數有限,就稱向量空間為有限維向量空間,將元素的個數稱作向量空間的維數。...
代數數域是數學中代數數論的基本概念,數域的一類,有時也被簡稱為數域,指有理數域 ℚ 的有限擴張形成的擴域。任何代數數域都可以視作 ℚ 上的有限維向量...
K。線性運算元的重要性在於它是向量空間之間的態射。在有限維情形下,線性運算元可以以下面的方式由矩陣表示。 設 是一個域, 和 是 上有限維向量空間。選擇一組基 ...
給定一個實矩陣 A,矩陣 A(T)A是A的列向量的格拉姆矩陣,而矩陣 AA(T)是A的行向量的格拉姆矩陣。對一般任何域上的有限維向量空間上的雙線性形式B,我們可對一...
線上性代數中,若爾當標準型(英語:Jordan normal form)或稱若爾當正規型(英語:Jordan canonical form)是某個線性映射在有限維向量空間上的特別的矩陣表達形式,稱作...
域多項式(field polynomial)一種特殊多項式.指在域擴張下,由一個元素所決定的多項式一個有限域擴張K/F,K可以看成F上的有限維向量空間.設w是它的一個基,對於x...
伯恩賽德基定理(Burnside basis theorem) p群的類似於有限維向量空間基底的一個定理.該定理斷言:若有限p群屍模去其弗拉梯尼子群}(P)的商群的階」P/}(P> }...
設G是有限群,V是複數域 C上的有限維向量空間,GL(V)是V上全體可逆線性變換所組成的群。從G 映入GL(V)的一個同態(見公式1 )稱為G的一個表示,而V稱為ρ...
對於有限維向量空間的自同態,其特徵多項式在地面場上分解成線性因子,Jordan-Chevalley分解存在並且對Jordan正規形式有簡單的描述。如果 是Jordan正規形式,則 是自同態,...
令(V,b)是不同於2的特徵的域k和非簡併對稱或偏斜對稱雙線性形式的有限維向量空間。 如果f:U→U'是V的兩個子空間之間的等值線,則f擴展到V的等值線。...
一個最經典的例子就是模論把域上的有限維向量空間的理論相當完美地推廣到主理想整環的情形, 建立了主理想整環上的有限生成模的理論。因此,無論是大學、專科還是...
向量空間,線性映射,矩陣;有限維向量空間,線性方程組,行列式,Cramer公式;多項式,有理分式,代數方程;矩陣的化簡,這些主題的選擇顯然反映了過去50年內數學的發展,但是...
(向量) 1.三維幾何學解釋: 就是根據物體的幾何性質而確定的一種定位方法.主要通過線性相關和線性變換解釋幾何問題 2.代數學: 在有限維向量空間中,也與線性相關...
