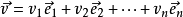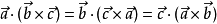矢量運算

矢量運算，矢量之間的運算要遵循特殊的法則。矢量加法一般可用平行四邊形法則。由平行四邊形法則可推廣至三角形法則、多邊形法則或正交分解法等。矢量減法是矢量加法的逆運算，一個矢量減去另一個矢量，等於加上那個矢量的負矢量。

基本介紹

• 中文名：矢量運算
• 套用學科：物理
• 適用領域範圍：矢量
• 適用領域範圍：標量

介紹

向量（英語：vector，物理、工程等也稱作矢量）是數學、物理學和工程科學等多個自然科學中的基本概念，指一個同時具有大小和方向，且滿足平行四邊形法則的幾何對象。一般地，同時滿足具有大小和方向兩個性質的幾何對象即可認為是向量（特別地，電流屬既有大小、又有正負方向的量，但由於其運算不滿足平行四邊形法則，公認為其不屬於向量）。向量常常在以符號加箭頭標示以區別於其它量。與向量相對的概念稱標量或數量，即只有大小、絕大多數情況下沒有方向（電流是特例）、不滿足平行四邊形法則的量。

向量的大小是相對的，在有需要時，會規定單位向量，以其長度作為1。每個方向上都有一個單位向量。

向量之間可以如數字一樣進行運算。常見的向量運算有：加法，減法，數乘向量以及向量之間的乘法（數量積和向量積）。

加法與減法

向量的加法滿足平行四邊形法則和三角形法則。具體地，兩個向量a和b相加，得到的是另一個向量。這個向量可以表示為a和b的起點重合後，以它們為鄰邊構成的平行四邊形的一條對角線，或者表示為將a的終點和b的起點重合後，從a的起點指向b的終點的向量：

兩個向量a和b的相減，則可以看成是向量a加上一個與b大小相等，方向相反的向量。又或者，a和b的相減得到的向量可以表示為a和b的起點重合後，從b的終點指向a的終點的向量：

當這兩個向量數值、方向都不同，基本向量時，向量和計算為

並且有如下的不等關係：

此外，向量的加法也滿足交換律和結合律。

向量與積

向量空間分為有限維向量空間與無限維向量空間。在有限維向量空間中，可以找到一組（有限個）向量，使得任意一個向量v都可以唯一地表示成這組向量的線性組合：

其中的標量是隨著向量v而確定的。這樣的一組向量稱為向量空間的基。給定了向量空間以及一組基後，每個向量就可以用一個數組來表示了。兩個向量v和w相同，若且唯若表示它們的數組一樣。

兩個向量v和w的和：

它們的數量積為：

而標量k與向量v的乘積則為：

標量乘法

一個標量k和一個向量v之間可以做乘法，得出的結果是另一個與v方向相同或相反，大小為v的大小的|k|倍的向量，可以記成。該種運算被稱為標量乘法或數乘。-1乘以任意向量會得到它的反向量，0乘以任何向量都會得到零向量0。

數量積

數量積也叫點積，它是向量與向量的乘積，其結果為一個標量（非向量）。幾何上，數量積可以定義如下：

設a、b為兩個任意向量，它們的夾角為，則他們的數量積為：

即a向量在b向量方向上的投影長度（同方向為正反方向為負號），與a向量長度的乘積。 數量積被廣泛套用於物理中，如做功就是用力的向量乘位移的向量，即 。

向量積

向量積也叫叉積，外積，它也是向量與向量的乘積，不過需要注意的是，它的結果是個向量。它的幾何意義是所得的向量與被乘向量所在平面垂直，方向由右手定則規定，大小是兩個被乘向量張成的平行四邊形的面積。所以向量積不滿足交換律。舉例來說 但是 。

設有向量，

則其向量積的矩陣表達式可用下列符號表示：

混合積

三個向量a、b和c的混合積定義為，物理意義為三向量始於同點時所構成的體積：

條件是：a,b,c 向量組成右手系，才為正數。

標積與矢積

一定要清晰地區分開標積與矢積。見下表。

名稱	標積 / 內積 / 數量級 / 點積	矢積 / 外積 / 向量積 / 叉積
運算式（a，b和c粗體字，表示向量）	a·b=|a||b|·cosθ	a×b=c,其中|c|=|a||b|·sinθ,c的方向遵守右手定則
幾何意義	向量a在向量b方向上的投影與向量b的模的乘積	c的模等於以a和b為鄰邊的平行四邊形的面積
運算結果的區別	標量（常用於物理）/數量（常用於數學）	矢量（常用於物理）/向量（常用於數學）