基本介紹
- 中文名:jordan-chevalley分解
- 外文名:Jordan–Chevalley decomposition
- 學科:數理科學
- 領域:代數群
定義,自同態分解,
定義
Jordan-Chevalley分解概念如下:




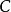
(1)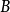 是個可對角化的矩陣;
是個可對角化的矩陣;
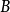
(2)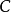 是個冪零陣;
是個冪零陣;
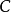
(3) ;
;

(4)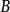 、
、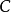 都可以表示為
都可以表示為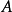 的多項式;
的多項式;
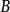
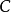
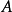
不僅如此,僅滿足(1)、(2)、(3)條件的分解就是唯一的。
自同態分解














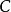
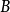
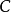

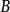
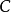
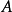










在數學方面,Jordan-Chevalley分解(Jordan–Chevalley decomposition),以Camille Jordan和Claude Chevalley的名字命名,表示線性運算元作為其通勤半單部分及其冪零部分的總和。...
Jordan-Chevalley分解Engel定理與Lie定理冪零線性李代數Killing型Cartan子代數Cartan準則典型李代數的Killing型與Cartan子代數第三章 復半單李代數的結構...
書中對一些問題的處理很有特色,立足點較高,但敘述十分清晰,如線性變換的Jordan-Chevalley分解、Cartan子代數的共軛定理、同構定理的證明、根系統的公理化處理、Weyl...
