基本介紹
- 中文名:線性變換
- 外文名:linear mapping
- 屬於:數學名詞
- 定義:線性空間V到W的保線性的映射
- 套用學科:數學
- 別名:線性映射
定義
 線性變換參考圖
線性變換參考圖性質
運算


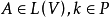
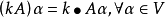



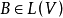
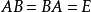
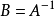
理解
 線性變換參考圖
線性變換參考圖 雙線性變換圖
雙線性變換圖 線性變換算式
線性變換算式 線性變換算式
線性變換算式 線性變換參考圖
線性變換參考圖
線性運算元一般指本詞條
 線性變換參考圖
線性變換參考圖

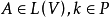
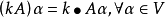



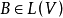
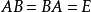
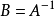
 線性變換參考圖
線性變換參考圖 雙線性變換圖
雙線性變換圖 線性變換算式
線性變換算式 線性變換算式
線性變換算式 線性變換參考圖
線性變換參考圖泛函分析中一種重要的運算元。運算元(映射)有線性和非線性之分.線性運算元又分為有界和無界兩類,有界線性運算元是線性賦范空問的基本概念。...
設[c,d]⊂[a,b], L是C[a,b]到C[c,d]的線性運算元,f∈C[a,b],記L(f)在點x∈[c,d]處的值為L(f,x),在[c,d]上用L(f,x)對f(x)的...
閉線性運算元(closed linear operator)是一種特殊的線性運算元,常直接稱為閉運算元。連續線性運算元必是閉運算元,但閉運算元不一定是連續運算元。根據閉圖像定理可知,定義域是閉...
單射線性運算元(injective linear operator)是一對一的線性運算元,有時也稱為內射線性運算元。...
設X是巴拿赫空間,T是X到X的線性運算元,定義域是𝓓(T)。若𝓡(T)=X,T是單射,且T-1是有界的,則稱T是正則線性運算元。...
設X,Y為賦范線性空間,T是線性運算元。如果𝓓(T)在X中是稠密的,則稱T是稠密線性運算元。...
共軛線性運算元(conjugate linear operator)是由線性運算元誘導出的共軛空間之間的運算元。...
滿射線性運算元亦稱為映到上的線性運算元,是值域等於全空間的線性運算元。...... 設T是線性賦范空問E的線性子空間D(T)到E的線性運算元,λ是一個實數,如果λI-T是D(...
線性微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。...... 線性微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。...
既是單射又是滿射的線性運算元稱為雙射線性運算元(bijective linear operator)。...... 滿射線性運算元是值域等於全空間的線性運算元,亦稱為映到上的線性運算元。...
相似線性運算元(similar linear operator)是相似矩陣的推廣,相似運算元具有相同的譜。...... 相似線性運算元(similar linear operator)是相似矩陣的推廣,相似運算元具有相同的譜...
運算元(英語:Operator)是從一個向量空間(或模)到另一個向量空間(或模)的映射。矩陣運算元是當需要建立從當前矩陣到特殊類型矩陣的映射時所使用的方法。...
有界n線性運算元是映有界集的n線性運算元。n線性運算元的有界性與連續性是等價的。...... 有界n線性運算元是映有界集的n線性運算元。n線性運算元的有界性與連續性是等價...
在數學中,微分運算元是定義為微分運算之函式的運算元。首先在記號上,將微分考慮為一個抽象運算是有幫助的,它接受一個函式得到另一個函式(以計算機科學中高階函式的...
可逆線性運算元是一種具有有界逆映射的線性運算元,是線性代數中可逆矩陣概念的一種推廣。...
線性映射( linear mapping)是從一個向量空間V到另一個向量空間W的映射且保持加法運算和數量乘法運算,而線性變換(linear transformation)是線性空間V到其自身的線性...
設X、Y均為距離空間,T為X→Y的線性運算元,如果T將X中的任一有界集映成Y中的列緊集,則T稱為緊運算元,連續的緊運算元稱作全連續運算元。如果X、Y均為賦范線性空間...
設X,Y同是數域K上的線性空間,D是X的線性子空間,T是從D到Y中的映射。如果對每個x,y∈D,有T(x+y)=Tx+Ty,則稱T是可加運算元。...
本書從有限維空間線性運算元的特徵值出發,採用類比、歸納等方式,通過大量實例循序漸進地引入無窮維空間上線性運算元的譜理論,系統介紹並分析了有界線性運算元、共軛運算元、...
所謂有界線性運算元空間,是指賦范線性空間X到賦范線性空間Y的有界線性運算元全體。...... 有界線性運算元是線性賦范空問的基本概念,是泛函分析中一種重要的運算元。...
《線性運算元譜理論及其套用》科學出版社2013-3出版。...... 《線性運算元譜理論及其套用》介紹線性運算元及其譜的基本概念,無界對稱運算元、J-對稱運算元和C-對稱運算元的擴張...
在數學裡,作用於一個有限維的內積空間,一個自伴運算元(self-adjoint operator)等於自己的伴隨運算元;等價地說,表達自伴運算元的矩陣是埃爾米特矩陣。埃爾米特矩陣等於自己...
線性運算元內插定理亦稱里斯凸性定理,是線性運算元有界性質的一個定理。...... 線性運算元內插定理亦稱里斯凸性定理,是線性運算元有界性質的一個定理。中文名 線性運算元內...
