基本介紹
- 中文名：位置矢量
- 外文名：(Position) Vector
- 適用範圍：數理科學
定義,說明,與位移的區別,矢量運算,相對位置矢量,相對坐標函式,
定義
位置矢量是在某一時刻，以坐標原點為起點，以運動質點所在位置為終點的有向線段。
仿射幾何學定義：A為仿射空間，若確定任意一點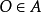
，則使
的A的元素p與V的元素α有一一對應的關係。這樣的α稱為以O為起點的p的位置矢量，以
表示。
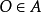
說明
①質點在參照系內選定坐標系中的位置矢量，是一根由坐標系原點指向質點所在位置的有向線段，如圖的r。
②對於直角坐標系，質點的位置矢量可用x、y、z來確定，其大小為
。其方向的餘弦分別為
，且
。
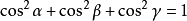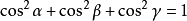
位置矢量與位移的區別
位矢描述的是在某一時刻運動質點在空間中的位置；而位移描述的是在某一時間間隔內運動質點位置變動的大小和方向。位矢與時刻相對應；位移與時間間隔相對應。
矢量運算
1. 矢量A和B相加定義為兩矢量的和，用新矢量A+B表示。用的平行四邊形法則或首尾相接法則進行
A和B相減定義為兩矢量的差，用新矢量A-B表示。寫為A-B=A +(-B)，按B反向再與A相加。
矢量的加（減）運算法則：
交換律：A+B=B+A；
結合律：A+B-C=A+(B-C)=(A+B)-C。
2. 標量ƒ與矢量A的乘積定義為一新矢量ƒA，它是A的ƒ倍。
3. 兩矢量A和B的標量積定義為標量 ，又稱為點積。其量值為兩矢量的模與兩矢量間夾角α (0≤α≤180°)的餘弦之積
特點：
（1）兩矢量的點積為一標量，其正、負取決於α是銳角還是鈍角；
（2）點積遵從交換律；
（3）A與B相互垂直，|A||B|cosα=0，反之亦然；
（4）在直角坐標下A、B的點積運算：將兩矢量的各分量逐項點乘。矢量的點積遵循分配率。
4. A和B的矢量積表示為A×B，又稱為叉積。
特點：
（1）兩矢量的叉積是一個矢量；
（2）叉積不遵從交換率，應是A×B=-(B×A)；
（3）A、B相平行（α= 0或180°）時，A×B=0，反之亦然------兩矢量平行的充要條件；
（4）A自身的叉積為零，即A×A=0。
相對位置矢量
相對位置矢量可表示空間任意兩點之間的位置關係。R是以P'點為起點、P點為終點的空間矢量，它的模表示P點相對於P'點的距離，它的方向表示P點相對於P'點所處的方位，則稱R為P點相對於P'點的相對位置矢量。
若考慮P'點相對於P點的相對位置矢量R'，則R'的方向是由P點指向P'點，有R'=-R。
任何真實的物理場，都有其產生的根源即所謂的場源，例如靜止電荷是靜電場的場源，恆定電流是恆定磁場的場源，等等。場源和它所產生的物理場總是與空間概念聯繫在一起的。以後我們將要研究的電磁場和它的源之間存在的關係，其中場源所在位置的點和需要確定場量（如電場強度矢量和磁場強度矢量）的點需要在名稱和符號上加以明確的區分。場源所在位置的點簡稱源點，用加撇的源點坐標 (x', y', z') 或r'表示；需要確定場量的點簡稱場點，用不帶撇的場點坐標（x, y, z）或r表示。於是，R就具有了場點相對於源點的相對位置矢量的特殊含義。
至於空間普通兩點的相對位置矢量，可通過加雙下標予以區別，如將P2點相對於P1點的相對位置矢量記為R12，其方向是由P1點指向P2點。
相對坐標函式
與相對位置矢量有關的一類函式，其變數為場點與源點的坐標差。相對坐標標量函式和相對坐標矢量函式分別記為
。
