在量子力學裡,位置算符(position operator)是一種量子算符。對應於位置算符的可觀察量是粒子的位置。位置算符的本徵值是位置矢量。
基本介紹
- 中文名:位置算符
- 外文名:position operator
- 學科:物理
詳解
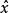


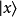

本徵函式
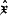
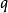
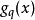
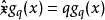

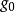
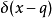
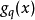


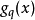

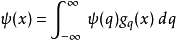
期望值
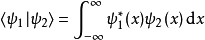
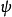

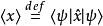
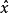
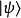
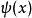

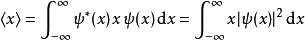

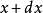
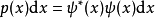

在量子力學裡,位置算符(position operator)是一種量子算符。對應於位置算符的可觀察量是粒子的位置。位置算符的本徵值是位置矢量。
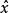


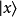

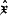
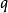
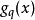
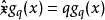

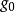
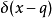
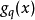


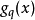

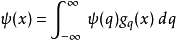
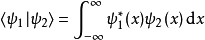
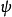

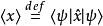
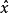
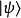
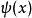

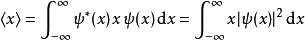

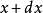
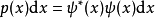
在量子力學裡,位置算符(position operator)是一種量子算符。對應於位置算符的可觀察量是粒子的位置。位置算符的本徵值是位置矢量。...
按照兩個檢索出現的順序相距離,可以有多種位置算符。而且對同一位置算符,檢索系統不同,規定的位置算符也不同。以美國DIALOG檢索系統使用的位置算符為例,介紹如...
向右移位時,最右邊的比特值會在邊界處“離開”,左邊的負數位標識符向右移動兩個位置,騰出來的空白位置用1來填充。最終結果是-2。(c語言中移位運算只能用於整數,...
位運算符用來對二進制位進行操作,Java中提供了如下表所示的位運算符:位運算符...將int型變數a的第k位置1, 即a=a|(1<<k)int型變數循環左移k次,即a=a<...
在量子力學裡,角動量算符(angular momentum operator)是一種算符,類比於經典的角動量。在原子物理學涉及旋轉對稱性(rotational symmetry)的理論里,角動量算符占有...
動量算符是在量子力學中表示微觀粒子的動量的算符。動量算符是表示力學量的厄米算符。...
視窗,單擊需要添加運算符的公式使其處於編輯狀態,並將插入條游標定位到目標位置...左 * / % 算數運算符 左 + - . 算數運算符和字元串運算符 左 << ...
非結合算符是指既不是左結合又不是右結合的算符。大多數語言並沒有分非結合...先以前面的運算符(即位置上處於左邊的運算符)構造運算, 就是左結合, 反之, ...
And 運算符還對兩個數值表達式中位置相同的位執行逐位比較,並根據下表設定 result 中相應的位:如expression1中的位是 且expression2 中的位是 則result為 0 ...
如名字表示的三元運算符需要三個運算元。語法為:條件表達式?表達式1:表達式2。說明:問號前面的位置是判斷的條件,判斷結果為bool型,為true時調用表達式1,為false時...
檢索式是檢索者向計算機發布的指令,也是人機對話的語言,檢索式表達了檢索者的檢索意圖。檢索式通常由檢索詞、邏輯算符、通配符等組成。...
鄰近檢索又稱位置算符檢索,用於規定命中的檢索詞在記錄中的間隔距離。最近鄰檢索就是根據數據的相似性,從資料庫中尋找與目標數據最相似的項目,而這種相似性通常會...
與Prewitt運算元相比,Sobel運算元對於像素的位置的影響做了加權,可以降低邊緣模糊程度,因此效果更好。Sobel運算元另一種形式是各向同性Sobel(Isotropic Sobel)運算元,也有兩個,...
這個在物理學中非常基本的概念.我們所說的場是指取決於 空間位置的一個量....劈形運算元在數學中用於指代梯度算符,並形成散度、旋度和拉普拉斯運算元。它也用於...
可以用來描述任意的歸一化後的圖像區域,是一個3D梯度位置方向直方圖,位置被量化到4×4局部柵格,梯度角度分為8個方向,運算元為4×4×8=128維。...
與Prewitt運算元相比,Sobel運算元對於象素的位置的影響做了加權,可以降低邊緣模糊程度,因此效果更好。Sobel運算元另一種形式是各向同性Sobel(Isotropic Sobel)運算元,也有兩個,...
