Sobel運算元

Sobel運算元

Sobel運算元是像素圖像邊緣檢測中最重要的運算元之一，在機器學習、數字媒體、計算機視覺等信息科技領域起著舉足輕重的作用。在技術上，它是一個離散的一階差分運算元，用來計算圖像亮度函式的一階梯度之近似值。在圖像的任何一點使用此運算元，將會產生該點對應的梯度矢量或是其法矢量。

基本介紹

  • 中文名：索貝爾運算元
  • 外文名：Sobel operator
  • 別稱：一階梯度運算元
  • 提出者：Irwin Sobel
  • 提出時間：二十世紀中後期
  • 套用學科：數學，圖像處理
  • 適用領域範圍：圖像處理，模式識別，機器視覺等
由來,核心公式,運算元描述,.NET代碼,C代碼,

由來

對於已經寫入數字圖像處理及機器視覺教科書多年的Sobel運算元，誰也沒曾追問和關心過它的發明背景和歷史。最近，給學生上“光電圖像處理”課，想介紹一下該運算元的來歷，查了很多文獻，就是找不到原始文獻。Google學術里搜尋，信息很多，卻不一致。有標註為期刊論文的，也有標註出版物析出的，出版時間也不一致（岡薩雷斯《Digital Image Processing》教材標註的時間為1970年）。
Irwin SobelIrwin Sobel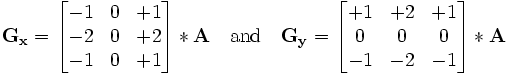
這個看似簡單，但領域內科研、開發人員沿用了幾十年的邊緣檢測運算元究竟如何產生的？偶然發現了一個帖子，該運算元的提出者Irwin Sobel在運算元產生多年後於該帖中詳細談到它的由來和定義。
原來，這個著名的Sobel邊緣運算元，當年作者並沒有公開發表過論文，僅僅是在一次博士生課題討論會(1968)上提出("A 3x3 Isotropic Gradient Operator for Image Processing")，後在1973年出版的一本專著（"Pattern Classification and Scene Analysis"）的腳註里作為注釋出現和公開的。
圖1 x和y兩個方向的sobel運算元模板圖1 x和y兩個方向的sobel運算元模板
圖2 灰度圖像sobel運算元處理效果圖圖2 灰度圖像sobel運算元處理效果圖

核心公式

該運算元包含兩組3x3的矩陣，分別為橫向及縱向，將之與圖像作平面卷積，即可分別得出橫向及縱向的亮度差分近似值。如果以A代表原始圖像，Gx及Gy分別代表經橫向及縱向邊緣檢測的圖像，其公式如下:
Sobel運算元
圖像的每一個像素的橫向及縱向梯度近似值可用以下的公式結合，來計算梯度的大小。
Sobel運算元
可用以下公式計算梯度方向。
Sobel運算元
在以上例子中，如果以上的角度Θ等於零，即代表圖像該處擁有縱向邊緣，左方較右方暗。

運算元描述

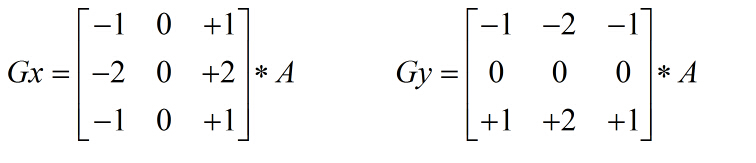
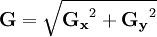
在邊緣檢測中，常用的一種模板是Sobel 運算元。Sobel 運算元有兩個，一個是檢測水平邊緣的 ；另一個是檢測垂直邊緣的 。與Prewitt運算元相比，Sobel運算元對於像素的位置的影響做了加權，可以降低邊緣模糊程度，因此效果更好。
Sobel運算元另一種形式是各向同性Sobel(Isotropic Sobel)運算元，也有兩個，一個是檢測水平邊緣的 ，另一個是檢測垂直邊緣的 。各向同性Sobel運算元和普通Sobel運算元相比，它的位置加權係數更為準確，在檢測不同方向的邊沿時梯度的幅度一致。將Sobel運算元矩陣中的所有2改為根號2，就能得到各向同性Sobel的矩陣。
由於Sobel運算元是濾波運算元的形式，用於提取邊緣，可以利用快速卷積函式， 簡單有效，因此套用廣泛。美中不足的是，Sobel運算元並沒有將圖像的主體與背景嚴格地區分開來，換言之就是Sobel運算元沒有基於圖像灰度進行處理，由於Sobel運算元沒有嚴格地模擬人的視覺生理特徵，所以提取的圖像輪廓有時並不能令人滿意。 在觀測一幅圖像的時候，我們往往首先注意的是圖像與背景不同的部分，正是這個部分將主體突出顯示，基於該理論，我們給出了下面閾值化輪廓提取算法，該算法已在數學上證明當像素點滿足常態分配時所求解是最優的。

.NET代碼

unsignedcharComputeSobel(unsignedcharul,//upperleftunsignedcharum,//uppermiddleunsignedcharur,//upperrightunsignedcharml,//middleleftunsignedcharmm,//middle(unused)unsignedcharmr,//middlerightunsignedcharll,//lowerleftunsignedcharlm,//lowermiddleunsignedcharlr,//lowerrightfloatfScale){shortHorz=ur+2*mr+lr-ul-2*ml-ll;shortVert=ul+2*um+ur-ll-2*lm-lr;shortSum=(short)(fScale*(abs((int)Horz)+abs((int)Vert)));if(Sum<0){return0;}elseif(Sum>0xff){return0xff;}return(unsignedchar)Sum;}for(Times=0;Times<128&&iThreshold!=iNewThreshold;Times++){iThreshold=iNewThreshold;lP1=0;lP2=0;lS1=0;lS2=0;for(i=iMinGray;i<iThreshold;i++){lP1+=Histogram*i;lS1+=Histogram;}iMean1Gray=lP1/lS1;for(i=iThreshold;i<iMaxGray;i++){lP2+=Histogram*i;lS2+=Histogram;}iMean2Gray=lP2/lS2;iNewThreshold=(iMean1Gray+iMean2Gray)/2;}//補充Sobel運算元的矩陣表達式：Sobel1=[-1-2-1;000;121];//檢測垂直邊沿的Sobel運算元Sobel2=[10-1;20-2;10-1];//檢測水平邊沿的Sobel運算元

C代碼

/* Sobel templatea00 a01 a02a10 a11 a12a20 a21 a22*/unsigned char a00, a01, a02;unsigned char a10, a11, a12;unsigned char a20, a21, a22;void MySobel(IplImage* gray, IplImage* gradient){CvScalar color ;for (int i=1; i<gray->height-1; ++i){for (int j=1; j<gray->width-1; ++j){a00 = cvGet2D(gray, i-1, j-1).val[0];a01 = cvGet2D(gray, i-1, j).val[0];a02 = cvGet2D(gray, i-1, j+1).val[0];a10 = cvGet2D(gray, i, j-1).val[0];a11 = cvGet2D(gray, i, j).val[0];a12 = cvGet2D(gray, i, j+1).val[0];a20 = cvGet2D(gray, i+1, j-1).val[0];a21 = cvGet2D(gray, i+1, j).val[0];a22 = cvGet2D(gray, i+1, j+1).val[0];// x方向上的近似導數  卷積運算double ux = a20 * (1) + a10 * (2) + a00 * (1)+ (a02 * (-1) + a12 * (-2) + a22 * (-1));// y方向上的近似導數  卷積運算double uy = a02 * (1) + a01 * (2) + a00 * (1)+ a20 * (-1) + a21 * (-2) + a22 * (-1);color.val[0] = sqrt(ux*ux + uy*uy);cvSet2D(gradient, i, j, color);}}}//注釋:該程式需要在安裝Opencv軟體下運行。Matlabps=imread('D:\14.jpg'); %讀取圖像subplot(1,3,1)imshow(ps);title('原圖像');ps=rgb2gray(ps);[m,n]=size(ps); %用Sobel微分運算元進行邊緣檢測pa = edge(ps,'sobel');subplot(1,3,2);imshow(pa);title('Sobel邊緣檢測得到的圖像');

相關詞條

熱門詞條

聯絡我們