基本介紹
套用領域
計算方法
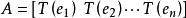

套用實例




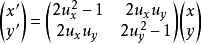

變換性質


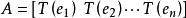





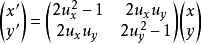


變換矩陣是數學線性代數中的一個概念。線上性代數中,線性變換能夠用矩陣表示。如果T是一個把Rn映射到Rm的線性變換,且x是一個具有n個元素的列向量 ,那么我們把m...
矩陣變換是線性代數中矩陣的一種運算形式。線上性代數中,矩陣的初等變換是指以下三種變換類型 :(1) 交換矩陣的兩行(對調i,j,兩行記為ri,rj);(2) 以一個非...
線性映射( linear mapping)是從一個向量空間V到另一個向量空間W的映射且保持加法運算和數量乘法運算,而線性變換(linear transformation)是線性空間V到其自身的線性...
線性變換矩陣(matrix of a linear transforma-tion)一種特殊矩陣。指該矩陣可以通過線性變換得到。...
仿射變換,又稱仿射映射,是指在幾何中,一個向量空間進行一次線性變換並接上一個平移,變換為另一個向量空間。仿射變換是在幾何上定義為兩個向量空間之間的一個仿射...
householder變換(Householder transformation),譯為“豪斯霍爾德變換”,或譯“豪斯霍德轉換”,又稱初等反射(Elementary reflection),最初由A.C Aitken在1932年提出。...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
基變換公式、基變換矩陣等 目錄 1 基本知識 2 相關定理 3 例題分析 基變換基本知識 編輯 在向量空間中,任一向量在指定基下的坐標是唯一的,但在不同基下的...
剪下變換(shear transformation)是空間線性變換之一,是仿射變換的一種原始變換。它指的是類似於四邊形不穩定性那種性質,方形變平行四邊形,任意一邊都可以被拉長的...
過渡矩陣是基與基之間的一個可逆線性變換,在一個空間V下可能存在不同的基。假設有2組基分別為A,B。由基A到基B可以表示為B=AP,過渡矩陣P=A^-1B。它表示...
二維幾何變換,二維指長和寬,即平面,二維幾何變換就是平面幾何的幾種變換,如平移,旋轉,翻折等的變換。...
初等變換(elementary transformation)是三種基本的變換,出現在《高等代數》中。初等變換包括:線性方程組的初等變換、行列式的初等變換和矩陣的初等變換,這三者在本質上...
吉文斯變換(Givens transformation)亦稱平面旋轉變換.數值代數的基本工具之一它是一種正交變換...
1. 作為一個合格 的變換,一定得形成一個變換矩陣。2. 在變換矩陣中,左邊作為原句式的一個個實例,形式必須相同,語法意義也必須一致。3. 在變換矩陣中,右邊的...
Denavit 和Hartenberg在1955年提出一種通用的方法,這種方法在機器人的每個連桿上都固定一個坐標系,然後用4×4的齊次變換矩陣來描述相鄰兩連桿的空間關係。通過依次...
希爾伯特矩陣是一種數學變換矩陣,正定,且高度病態(即,任何一個元素髮生一點變動,整個矩陣的行列式的值和逆矩陣都會發生巨大變化),病態程度和階數相關。...
沃爾什變換(Walsh transform) 以沃爾什函式為基本函式的一種非正弦正交變換。...... 由於按哈達瑪編號的沃爾什變換(WHT)其變換矩陣具有簡單的遞推關係,且正、反變換...
當需要建立從當前矩陣到特殊類型矩陣的映射時,就用到線性運算元的矩陣(簡稱運算元矩陣)。例如從矩陣到對角矩陣的變換,用到相似變換矩陣。...
《矩陣理論》,是2006年科學出版社出版的圖書,作者是蘇育才、姜翠波、張躍輝。主要介紹線性空間與線性變換、內積空間與等距變換、特徵值與特徵向量、λ-矩陣與Jordan...
Arnold變換可以看作是拉伸,壓縮,摺疊及拼接的過程。通過這一過程將離散化的數字圖像矩陣中的點重新排列。設像素的坐標,Arnold變換為: 此變換稱為二維Arnold變換,...
Hadamard變換作為變換編碼的一種在視頻編碼當中使用有很久的歷史,在視頻編碼標準中,Hadamard變換多被用來計算SATD(一種視頻殘差信號大小的衡量)。...
變換法(transformation method)一類常用的解特徵值問題的數值方法.其基本點是利用三類基本變換 。...
數字圖像數據可以用矩陣來表示,因此可以採用矩陣理論和矩陣算法對數字圖像進行分析和處理。由於數字圖像可以表示為矩陣的形式,所以在計算機數字圖像處理程式中,通常用...
矩陣相乘最重要的方法是一般矩陣乘積。它只有在第一個矩陣的列數(column)和第二個矩陣的行數(row)相同時才有意義。一般單指矩陣乘積時,指的便是一般矩陣乘積。...
