基本介紹
- 中文名:仿射變換
- 外文名:affine transformation
- 組成:由一個線性變換接上一個平移
- 描述:二維仿射變換的功能
- 別稱:仿射映射
- 套用學科:數學
定義
一般定義






其他定義



假設選定一原點




給定同一場中的兩個仿射空間


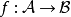

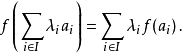
表示

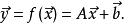


性質





實例
實數
有限域









於是, {a′} = y7 + y6 + y5 + y3 + y2 + 1 = {11101101} = {ED}。
平面幾何

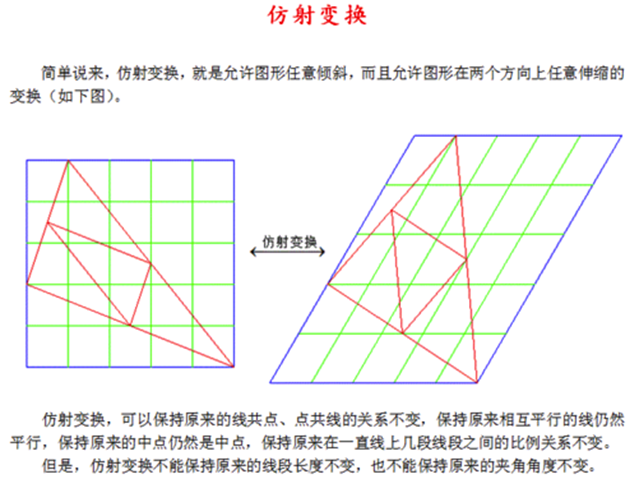















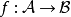

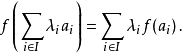

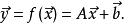

















仿射變換,又稱仿射映射,是指在幾何中,一個向量空間進行一次線性變換並接上一個平移,變換為另一個向量空間。仿射變換是在幾何上定義為兩個向量空間之間的一個仿射...
等積仿射變換亦稱麼模仿射變換,是一種特殊的仿射變換,指變積係數的絕對值等於1的仿射變換。...
仿射幾何學(affine geometry)是幾何學的一個分支。屬於高等數學的一種。主要套用於測量,建築,攝影等等。...
中心仿射變換(central affine transformation)是一類重要的仿射變換,指含一個不變點的仿射變換。位似變換是中心仿射變換的特例。...
仿射等價(affine equivalence)是圖形間的一種等價關係。若存在一個仿射變換把圖形C1變成C2,則稱C1與C2仿射等價。否則稱為仿射不等價。圖形的仿射等價是一種等價關係...
仿射對應(affine correspondence)是一種重要的幾何對應,是有限個透視仿射對應的乘積。例如,設有n+1個平面α,α1,α2,…,αn-1,β。如果在平面偶(α,α1),...
仿射不變數(affine invariant)是仿射變換的一種特徵,指圖形經過任何仿射對應(變換)都不改變的量。共線三點的單比是最基本、最重要的仿射不變數,其他如兩平行的有...
圖形的相似變換是指由一個圖形到另一個圖形,在改變的過程中保持形狀不變(大小方向和位置可變)的圖形。...
單碼加密法的另一種形式稱為仿射加密法(affine cipher)。在仿射加密法中,字母表的字母被賦予一個數字,例如a=0,b=1,c=2…z=25。仿射加密法的密鑰為0-25...
由有限次中心射影的積定義的兩條直線間的一一對應變換稱為一維射影變換。由有限次中心射影的積定義的兩個平面之間的一一對應變換稱為二維射影變換。因為正交變換...
變換矩陣是數學線性代數中的一個概念。線上性代數中,線性變換能夠用矩陣表示。如果T是一個把Rn映射到Rm的線性變換,且x是一個具有n個元素的列向量 ,那么我們把m...
仿射法線(affine normal line)是歐氏空間中曲面法線的推廣,與仿射空間中的超曲面橫截相交的直線,它是歐氏曲面論中法線的仿射類似。歐氏空間既是幾何學的研究對象,...
變換群是幾何學研究的重要對象。即由變換構成的群。設G是集合S的一一變換所構成的集合,若它滿足:1.集合內任二變換之積仍屬於這集合;2.集合內任一變換的逆變換...
介紹 仿射性質(affine property)仿射變換的一種特徵.指圖形經過任何仿射對應(變換)都不改變的性質.例如,同素性、結合性、平行性等都是仿射性質. ...
仿射微分幾何學(affine ldifferential geometry)是一門古典的微分幾何,屬於微分幾何學的一個分支,從屬於仿射變換群。內容包括曲線和曲面在仿射變換群下的不變數、協...
仿射函式,即最高次數為1的多項式函式。常數項為零的仿射函式稱為線性函式。...... ,稱為仿射變換(affine transform)或仿射映射(affine map),其中 A 是一個 矩陣...
仿射坐標系(affine coordinate system)是解析幾何中仿射坐標系的推廣。設V是實n維線性空間,A是關於V的仿射空間,A中一個固定點O與V的一個基(e1,e2,e3)稱為A...
仿射空間是數學中的幾何結構,這種結構是歐式空間的仿射特性的推廣。在仿射空間中,點與點之間做差可以得到向量,點與向量做加法將得到另一個點,但是點與點之間不...
仿射非線性系統是種特定的非線性系統。仿射非線性系統的能控制項問題,利用向量場族對應的積分曲線定義系統的能控制項。仿射非線性系統,這類系統對控制是線性的,使其動態...
仿射微分幾何基本定理(fundamental theoremof affine differential geometry)關於仿射空間中的超曲面完全由布拉施克度量和富比尼一皮克形式確定的定理.設在一個n維單連通...
n維射影變換(n-dimensional projective transformation)亦稱n維直射對應,是一類n維變換。指Pn中的一一對應。...
把直線(平面)上的點經過平行投影到另一直線(平面)上,這樣得到的點與點間的對應稱為“平行透視”,把一個圖形經過有限次平行透視後變成另一個圖形時,叫作“仿射...
《仿射微分幾何》內容簡介:仿射微分幾何是一門發展較早的學科。《仿射微分幾何》著者從20世紀20年代中期到30年代初期在這一學科中做了大量工作。《仿射微分幾何》...
AffineTransform 類表示 2D 仿射變換,它執行從 2D 坐標到其他 2D 坐標的線性映射,保留了線的“直線性”和“平行性”。可以使用一系列平移 (translation)、縮放 (...
