基本介紹
- 中文名:透視仿射對應
- 外文名:perspective affine correspondence
- 別稱:平行投影
- 所屬學科:數學
- 所屬問題:高等幾何(仿射幾何)
基本介紹
 圖1
圖1透視仿射對應的分類
同一平面內直線a到直線a'的一種對應關係
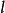
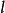
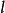
 圖2
圖2空間兩個平面間的透視仿射對應

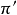


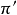


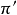

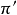

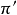

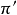


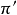
 圖3
圖3透視仿射對應的性質
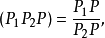




 圖1
圖1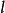
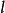
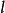
 圖2
圖2
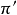


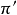


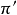

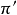

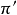



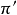
 圖3
圖3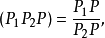



把直線(平面)上的點經過平行投影到另一直線(平面)上,這樣得到的點與點間的對應稱為“平行透視”,把一個圖形經過有限次平行透視後變成另一個圖形時,叫作“仿射...
又稱沙爾定律。透視旋轉定律是指利用平行四邊形原理,在糾正儀或其它攝影測量儀器上,轉動底片面或承影面,底片面與承影面間的透視對應關係不變的規律。...
仿射對應(affine correspondence)是一種重要的幾何對應,是有限個透視仿射對應的乘積。例如,設有n+1個平面α,α1,α2,…,αn-1,β。如果在平面偶(α,α1),...
定理平行射影(透視仿射對應)保持共線三點的單比不變 [3] 。單比交比 單比是仿射變換的基本不變數,但對於中心射影來說,單比不是不變數,它的基本不變數是交...
第1章仿射變換 1.1透視仿射對應與仿射變換 1.2仿射變換的性質 1.3仿射變換的代數形式 1.4仿射變換的簡單套用 第2章射影變換 2.1圓錐曲線的直觀定義...
第一章 仿射坐標與仿射變換§1 透視仿射對應§2 仿射對應與仿射變換§3 仿射坐標3.1 仿射坐標系3.2 仿射變換的代數表示3.3 幾種特殊的仿射變換...
第一章 仿射坐標與仿射變換1 透視仿射對應2 仿射對應與仿射變換3 仿射坐標4 仿射性質習題5 本章小結綜合練習題第二章 射影平面1 射影直線和射影平面習題...
一、知識點歸納§1 透視仿射對應§2 仿射對應與仿射變換§3 仿射坐標§4 仿射性質二、典型例題分析三、習題全解四、同步練習題精選:第二章 射影平面...
Φ上所有子午線是全同的,因而每條子午線的正面投影m''透視仿射對應於m''0。Φ在P0點的切平面τ0包含有P0處p和m0的切線,於是τ0反映為直線τ''0。繞a旋轉時...
也稱透視旋轉定律。利用平行四邊形原理,在糾正儀或其他攝影測量儀器上,轉動底片面或承影面,底片面與承影面間的透視對應關係不變的規律。...
1.1平行射影與仿射對應 1.2仿射不變性與不變數 1.3平面到自身的透視仿射 1.4平面內的一般仿射 1.5仿射變換的代數表示 第一章習題...
