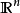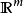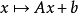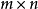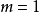仿射函式

仿射函式，即最高次數為1的多項式函式。常數項為零的仿射函式稱為線性函式。

基本介紹

• 中文名：仿射函式
• 外文名：affine function
• 概述 ：deg(f（x）)=1的函式稱為
• 說明：仿射函式即由1階多項式構成
• 區別：仿射函式即由由1階多項

定義

從 到 的映射，稱為仿射變換（affine transform）或仿射映射（affine map），其中 A 是一個 矩陣，b 是一個 m 維向量。當 時，稱上述仿射變換為仿射函式。

詳解

仿射函式即由 1 階多項式構成的函式，一般形式為 f(x)=Ax+b，這裡，A 是一個 m×k 矩陣，x 是一個 k 向量，b是一個 m 向量，實際上反映了一種從 k 維到 m 維的空間映射關係。

設 f 是一個矢性（值）函式，若它可以表示為 f(x₁,x₂,…,x_n)=A₁x₁+A₂x₂+…+A_nx_n+b，其中 A_i 可以是標量，也可以是矩陣，則稱 f 是仿射函式。其中的特例是，標性（值）函式 f(x)=ax+b ，其中a、x、b都是標量。此時嚴格講，只有 b=0 時，仿射函式才可以叫“線性函式”（“正比例”關係）。

就一般情形，函式f是仿射函式的充要條件是：對於任意兩組向量x₁,x₂,…,x_n與 y₁,y₂,…,y_n，對於任意0≤p≤1，如果 f[px₁+(1-p)y₁,px₂+(1-p)y₂,…,px_n+(1-p)y_n]≡pf(x₁,x₂,…,x_n)+(1-p)f(y₁,y₂,…,y_n)。

一般稱線性組合p₁x₁+p₂x₂+…+p_nx_n，其中 p₁+p₂+…+p_n=1 為仿射組合；一般稱所有 p_i≥0 的仿射組合為凸組合。其實一般意義上的仿射函式是一個矩陣函式，如果構成一個類似 LMI 的不等式，可以成為仿射矩陣不等式。

辨析

仿射函式和線性函式的區別

仿射函式即由 1 階多項式構成的函式，一般形式為 f (x) = A x + b，這裡，A 是一個 m×k 矩陣，x 是一個 k 向量，b 是一個 m 向量，實際上反映了一種從 k 維到 m 維的空間映射關係。

設 f 是一個矢性（值）函式，若它可以表示為 f(x₁,x₂,…,x_n)=A₁x₁+A₂x₂+…+A_nx_n+b，其中 A_i可以是標量，也可以是矩陣，則稱 f 是仿射函式。其中的特例是，標性（值）函式 f(x)=ax+b ，其中 a、x、b 都是標量。此時嚴格講，只有 b=0 時，仿射函式才可以叫“線性函式”（“正比例”關係）。