基本介紹
初等數學用法
 紅、藍直線斜率相同,紅、綠直線 y截距相同
紅、藍直線斜率相同,紅、綠直線 y截距相同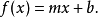




高等數學用法


 非線性函式
非線性函式線性關係






套用




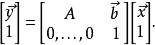

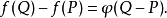
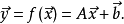

 紅、藍直線斜率相同,紅、綠直線 y截距相同
紅、藍直線斜率相同,紅、綠直線 y截距相同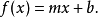






 非線性函式
非線性函式









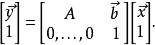

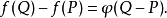
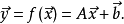
在數學裡,線性函式是指那些線性的函式,但也常用作一次函式的別稱,儘管一次函式不一定是線性的(那些不經過原點的)。線型函式是一個比較恰當的同義詞。...
線性特性是卷積運算的性質之一,即設a,b為任意常數,則對於函式f(z,y),h(x,y)和g(x,y),{af(x,Y)+bh(z,y)}*g(z,y)=-af(x,y)*g(x,y)+bh...
線性函式是一次函式的別稱,則非線性函式即函式圖像不是一條直線的函式。非線性函式包括指數函式、冪函式、對數函式、多項式函式等等基本初等函式以及他們組成的複合函式...
線性方程也稱一次方程式。指未知數都是一次的方程。其一般的形式是ax+by+...+cz+d=0。線性方程的本質是等式兩邊乘以任何相同的非零數,方程的本質都不受影響。...
在實數域內形如y=(cx+d)/(ax+b)的函式稱為分式線性函式...... 在實數域內形如y=(cx+d)/(ax+b)的函式稱為分式線性函式 中文名 分式線性函式 外文名 ...
線性回歸是利用數理統計中回歸分析,來確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法,運用十分廣泛。其表達形式為y = w'x+e,e為誤差服從均值為0...
兩個變數之間存在一次方函式關係,就稱它們之間存在線性關係。正比例關係是線性關係中的特例,反比例關係不是線性關係。更通俗一點講,如果把這兩個變數分別作為點的...
線性型又稱線性函式或線性齊次,是域F上的線性空間V到域F上的一個線性映射。線性映射(也叫做線性變換或線性運算元)是在兩個向量空間之間的函式,它保持向量加法和...
定義介紹 多重線性函式(multilinear function)一種特殊的多重線性映射.即當映射空間W為域K時的多重線性映射.有些作者把一般多重線性映射也稱為多重線性函式. ...
線性特性是卷積運算的性質之一,即設a,b為任意常數,則對於函式f(z,y),h(x,y)和g(x,y),{af(x,Y)+bh(z,y)}*g(z,y)=-af(x,y)*g(x,y)+bh...
在初級代數與解析幾何,線性函式是只擁有一個變數的一階多項式函式。因為,採用直角坐標系,這些函式的圖形是直線,所以,這些函式是線性的。線型函式是一個比較恰當的...
在數學中,線性化可以找到給定點處函式的線性逼近。 在動力學系統的研究中,線性化是一種評估非線性微分方程或離散動力系統平衡點局部穩定性的方法。 該方法用於工程...
線性回歸方程是利用數理統計中的回歸分析,來確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法之一。線性回歸也是回歸分析中第一種經過嚴格研究並在實際...
許多實際問題都用函式y=f(x)來表示內在規律的數量關係,其中相當一部分函式是通過實驗或觀測得到的。雖然f(x)在[a,b]上是存在的,有的還是連續的,但只能給出[...
線性規則 linear programming 具有非線性約束條件或目標函式的數學規劃,是運籌學的一個重要分支。...
一般的線性模型是以參數b)為係數的廣義多項式,即 (3)式中g0,g1,…,gn稱為基函式。對諸gj的不同選取可構成多種典型的和常用的線性模型。從函式逼近的觀點...
形如y'+P(x)y=Q(x)的微分方程稱為一階線性微分方程,Q(x)稱為自由項。一階,指的是方程中關於Y的導數是一階導數。線性,指的是方程簡化後的每一項關於y...
簡單來講,線性微分方程是指關於未知函式及其各階導數都是一次方,否則稱其為非線性微分方程。...
在數學中,雙曲函式是一類與常見的三角函式(也叫圓函式)類似的函式。最基本的雙曲函式是雙曲正弦函式sinh和雙曲餘弦函式cosh,從它們可以導出雙曲正切函式tanh等,...
