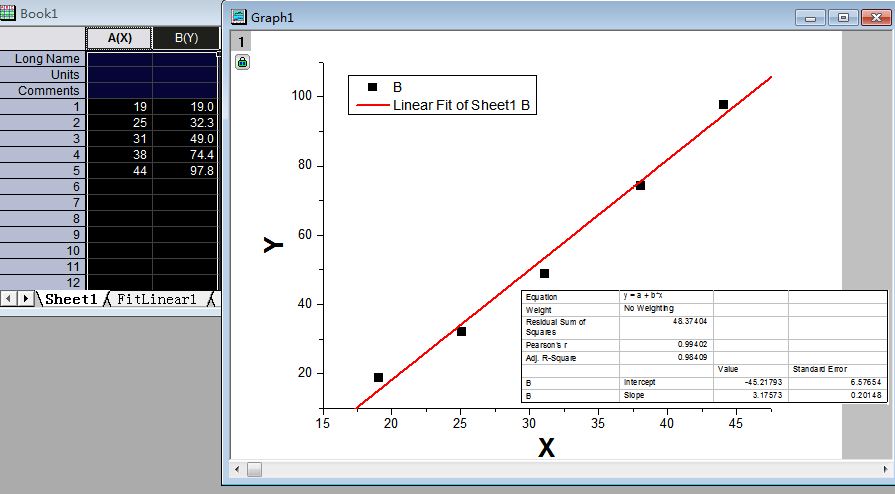
一般定義
線性關係的顯著特徵是圖像為過原點的直線(沒有常數項的情況下,如:y=kx+jz,(k,j為常數,x,z為變數);而當圖像為不過原點的直線時,函式稱為
直線關係。
線性關係與直線關係是兩不同的,經常被大家搞混淆。
首先每一項(
常數項除外)的次數必須是一次的(這是最重要的)
如:x=y+z+c+v+b
那么就說他們(x與y,z,c,v,b都是變數)是線性關係,可以說成:x與y是線性關係,或y與z是線性關係等等,
如果每項的
次數不是一次就不是線性關係:x=y*z(這裡假定y,z是
變數而不是
常數),那么x與y,或x與z就不是線性關係,
常數對是否構成直線關係沒影響(假定常數不為0)如:x=k*y+l*z+a(k,l是常數,y,z是變數,a是常數)那么x與y,z還是線性的,因為項:k*y是一次的,l*z這項也是一次的,
常數項a沒影響.
如:x=7*y+8*z是線性的,x=-y-2*z是線性的。x=2*y*z是非線性的(因為2yz這一項不是一次的),
從
二維圖像來講(假定只有y跟x這兩個變數),線性的方程一定是直線的,曲的不行,有轉折的也不行。
向量的線性表示
給定
向量組
A:
α1,
α2,…
αn,伐以及向量
b,若存在一組數k
1,k
2,…,kn,使得
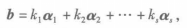 向量的線性關係
向量的線性關係則稱向量
b可由向量組
A線性表示,也稱向量
b是向量組
A的一個
線性組合,k
1,k
2,…,kn稱為這個線性組合的
係數.
向量b可由向量組A線性表示,也就是線性方程組
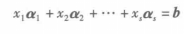 向量的線性關係
向量的線性關係有解.
設有向量組A:α1,α2,…αn,和B:β1,β2,…,βn,若向量組B中的每一個向量都可由向量組A線性表示,則稱向量組B可由向量組A線性表示;如果向量組A和向量組B能互相線性表示,則稱這兩個向量組等價,記作A≌B.
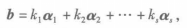 向量的線性關係
向量的線性關係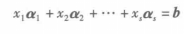 向量的線性關係
向量的線性關係