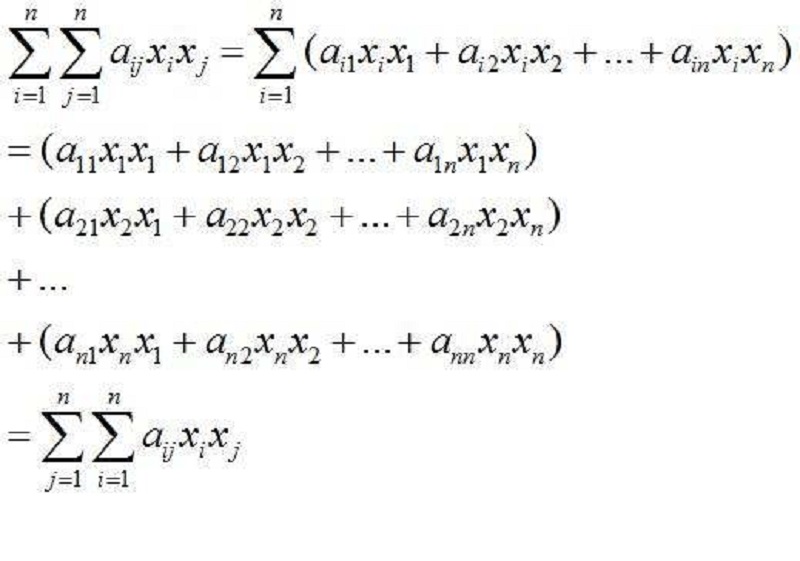線性型

線性型又稱線性函式或線性齊次，是域F上的線性空間V到域F上的一個線性映射。線性映射（也叫做線性變換或線性運算元）是在兩個向量空間之間的函式，它保持向量加法和標量乘法的運算。

兩個變數之間存在一次方函式關係，就稱它們之間存線上性關係。正比例關係是線性關係中的特例，反比例關係不是線性關係。

基本介紹

• 中文名：線性型
• 外文名：linear model
• 學科：數理科學
• 類型：數學術語
• 又稱：線性函式或線性齊次
• 線性映射：兩個向量空間之間的函式

定義

線性型又稱線性函式或線性齊次，是域F上的線性空間V到域F上的一個線性映射。如果f是從V到F的映射，對V的向量x，y，F的元素a，b滿足f(ax+by)=af(x)+bf(y),那么f就稱為V上的線性型或線性映射。

若e1，e2，……，en是V的一組基，則V的每一個向量x都可以表示成x=x1e1+x2e2+……xnen，式中xi在F域中，i=1,2，……，n。因此對於V上的線性型f有f(x)=x1f(e1)+x2f(e2)+……+xnf(en)或記成f(x1,x2,……,xn)=a1x1+a2x2+……+anxn，式中f(ei)=ai，i=1,2,……,n。

線性關係

兩個變數之間存在一次方函式關係，就稱它們之間存線上性關係。正比例關係是線性關係中的特例，反比例關係不是線性關係。更通俗一點講，如果把這兩個變數分別作為點的橫坐標與縱坐標，其圖象是平面上的一條直線，則這兩個變數之間的關係就是線性關係。即如果可以用一個二元一次方程來表達兩個變數之間關係的話，這兩個變數之間的關係稱為線性關係，因而，二元一次方程也稱為線性方程。推而廣之，含有n個變數的一次方程，也稱為n元線性方程，不過這已經與直線沒有什麼關係了。

數學中 Y=k*X (k為常數)，Y和X就是線性關係。

線性映射

線性空間V到自身的映射通常稱為V上的一個變換。

線性變換參考圖

同時具有以下定義：

線性空間V上的一個變換A稱為線性變換，如果對於V中任意的元素α，β和數域P中任意k，都有

A(α+β)=A（α）+A（β）

A (kα)=kA(α)

線性代數研究的一個對象，即向量空間到自身的保運算的映射。例如，對任意線性空間V，位似是V上的線性變換，平移則不是V上的線性變換。對線性變換的討論可藉助矩陣實現。σ關於不同基的矩陣是相似的。Kerσ={a∈V|σ（a）=θ}（式中θ指零向量）稱為σ的核，Imσ={σ（a）|a∈V}稱為σ的象，是刻畫σ的兩個重要概念。

對於歐幾里得空間，若σ關於標準正交基的矩陣是正交（對稱）矩陣，則稱σ為正交（對稱）變換。正交變換具有保內積、保長、保角等性質，對稱變換具有性質：〈σ(a)，β〉=〈a，σ（β）〉。

在數學中，線性映射（也叫做線性變換或線性運算元）是在兩個向量空間之間的函式，它保持向量加法和標量乘法的運算。術語“線性變換”特別常用，尤其是對從向量空間到自身的線性映射(自同態)。

在抽象代數中，線性映射是向量空間的同態，或在給定的域上的向量空間所構成的範疇中的態射。

例題

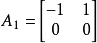在中，求在基，，，下的坐標。

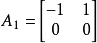
線上性空間中，滿足線性型關係。設所求坐標為：

則

即，

所以，。