n 次型亦稱n線性型(n-linear operator)。不同的 n 線性運算元可對應於相同的 n 次型。
基本介紹
- 中文名:n線性運算元
- 外文名:n-linear operator
- 適用範圍:數理科學
簡介
n線性運算元

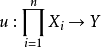
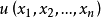
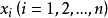
定義


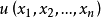





n 次型亦稱n線性型(n-linear operator)。不同的 n 線性運算元可對應於相同的 n 次型。

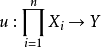
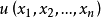
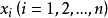


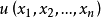





n 次型亦稱n線性型(n-linear operator)。不同的 n 線性運算元可對應於相同的 n 次型。...
完全形與初等幾何中的n邊形沒有任何共同之處,對於給定的n個點(其中無三點共線)或n條線(其中無三線共點),由其決定的完全n點形或完全n線形是惟一的 [2] ...
齊次線性方程組:常數項全部為零的線性方程組。如果m<n(行數小於列數,即未知數的數量大於所給方程組數),則齊次線性方程組有非零解,否則為全零解。...
有界n線性運算元是映有界集的n線性運算元。n線性運算元的有界性與連續性是等價的。...... 有界n線性運算元是映有界集的n線性運算元。n線性運算元的有界性與連續性是等價...
在計算複雜性理論,一個被稱為線性時間或 Ο(n)時間的算法,表示此算法解題所需時間正比於輸入資料的大小,通常以n表示。換句話說,執行時間與輸入資料大小為線性...
N型熱電偶nickel-chromium-silicon alloy / nickelchromium-。...... 4、在400~1300℃範圍內,N型熱電偶的熱電特性的線性比K型偶要好;5、在低溫範圍內(-200~...
常用的線性參數估計算法有LS、WLS、Ransac LS、LMedS(其實Ransac的使用並不局限於...其中疊代次數N是由樣本集子中樣本的個數、期望的模型誤差、事先估計的樣本中...
n階線性常微分方程(linear differential equation of n-th order)是未知函式導數最高階數為n的線性常微分方程。...
是n 個獨立觀測,服從指數型分布,即其有密度函式:其中 和 為參數, 和 為函式...聯繫函式確定了廣義線性模型的均值結構,對於不同的數據類型,不同的聯繫函式的...
線性電子電路目錄 編輯 1 半導體器件1.1 半導體導電特性1.2 PN結與導體二極體PN結(PN junction)。採用不同的摻雜工藝,通過擴散作用,將P型半導體與N型半導體製作在...
線性搜尋實例 編輯 int seqsearch(int list[], int searchnum, int n){int i;list[n] = searchnum; //把搜尋值放到最後一個位置,簡化代碼...
線性外推法可以很好地避免多項式外推法中隨意選取n值的弊端。當kro與So呈上凸型的曲線時,n值的選取範圍為0~1,這種情況極為少見。...
(2)多自由度系統的線性振動是自由度n≥2的線性系統的振動。一個n自由度系統有n個固有頻率和n個主振型。系統的任何振動形態都可以表成各個主振型的線性組合。...
高階線性雙曲型方程(higher order linear hy- perbolic equation)一類重要的高階方程.高階線性雙曲型方程有兩種定義.考慮n+1個變數((t,x> 的N階常係數線性...
