基本介紹
- 中文名:線性估計
- 外文名:nonlinear estimation
- 學科:數學
線性估計模型
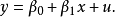
估計方法
WLS既是帶權重的最小方差,其思想是將每個輸入的樣本賦予權值,初始時每個樣本的權值相等,然後使用所有帶權重的樣本估計模型的參數,得到參數後,計算每個樣本與模型的偏差,再根據偏差決定樣本的新權重,偏差越大則權重越小,然後重複模型參數估計與權重更新這個過程,直到樣本的帶權偏差和收斂為止。
Ransac是一種隨機參數估計算法。Ransac LS從樣本中隨機抽選出一個樣本子集,使用LS對這個子集計算模型參數,然後計算所有樣本與該模型的偏差,再使用一個預先設定好的閾值與偏差比較,當偏差小於閾值時,該樣本點屬於模型內樣本點(inliers),否則為模型外樣本點(outliers),記錄下當前的inliers的個數,然後重複這一過程。每一次重複,都記錄當前最佳的模型參數,所謂最佳,既是inliers的個數最多,此時對應的inliers個數為best_ninliers。每次疊代的末尾,都會根據期望的誤差率、best_ninliers、總樣本個數、當前疊代次數,計算一個疊代結束評判因子,據此決定是否疊代結束。疊代結束後,最佳模型參數就是最終的模型參數估計值。
LMedS也是一種隨機參數估計算法。LMedS也從樣本中隨機抽選出一個樣本子集,使用LS對子集計算模型參數,然後計算所有樣本與該模型的偏差。但是與Ransac LS不同的是,LMedS記錄的是所有樣本中,偏差值居中的那個樣本的偏差,稱為Med偏差(這也是LMedS中Med的由來),以及本次計算得到的模型參數。由於這一變化,LMedS不需要預先設定閾值來區分inliers和outliers。重複前面的過程N次,從中N個Med偏差中挑選出最小的一個,其對應的模型參數就是最終的模型參數估計值。其中疊代次數N是由樣本集子中樣本的個數、期望的模型誤差、事先估計的樣本中outliers的比例所決定。

