基本介紹
- 中文名：線性判別分析
- 外文名：linear discriminant analysis
- 領域：機器學習
- 作用：分類、降維
- 提出者：Fisher
- 基本思想：將樣例投影到一條直線上
簡介,優點,套用領域,
簡介
線性判別分析是一種經典的線性學習方法，在二分類問題上最早由Fisher在1936年提出，亦稱Fisher線性判別。線性判別的思想非常樸素：給定訓練樣例集，設法將樣例投影到一條直線上，使得同類樣例的投影點儘可能接近，異樣樣例的投影點儘可能遠離；在對新樣本進行分類時，將其投影到同樣的直線上，再根據投影點的位置來確定新樣本的類別。LDA與方差分析（ANOVA）和回歸分析緊密相關，這兩種分析方法也試圖通過一些特徵或測量值的線性組合來表示一個因變數。然而，方差分析使用類別自變數和連續數因變數，而判別分析連續自變數和類別因變數（即類標籤）。邏輯回歸和機率回歸比方差分析更類似於LDA，因為他們也是用連續自變數來解釋類別因變數的。LDA的基本假設是自變數是常態分配的，當這一假設無法滿足時，在實際套用中更傾向於用上述的其他方法。LDA也與主成分分析（PCA）和因子分析緊密相關，它們都在尋找最佳解釋數據的變數線性組合。LDA明確的嘗試為數據類之間不同建立模型。 另一方面，PCA不考慮類的任何不同，因子分析是根據不同點而不是相同點來建立特徵組合。判別的分析不同因子分析還在於，它不是一個相互依存技術：即必須區分出自變數和因變數（也稱為準則變數）的不同。在對自變數每一次觀察測量值都是連續量的時候，LDA能有效的起作用。當處理類別自變數時，與LDA相對應的技術稱為判別反應分析。
優點
Fisher提出LDA距今已近七十年，仍然是降維和模式分類領域套用中最為廣泛採用而且極 為有效的方法之一，其典型套用包括人臉檢測、人臉識別、基於視覺飛行的地平線檢測、目標跟蹤和檢測、信用卡欺詐檢測和圖像檢索、語音識別等。之所以有如此廣泛的套用，其 主要原因是，LDA（包括其多類推廣）具有以下優點：可以直接求得基於廣義特徵值問題的解析解，從而避免了在一般非線性算法中，如多層感知器，構建中所常遇到的局部最小問題無需對模式的輸出類別進行人為的編碼，從而使 LDA 對不平衡模式類的處理表現出尤其明顯的優勢。與神經網路方法相比，LDA 不需要調整參數，因而也不存在學習參數和最佳化權重以及神經元激活函式的選擇等問題；對模式的歸一化或隨機化不敏感，而這在基於梯度 下降的各種算法中則顯得比較突出。在某些實際情形中，LDA 具有與基於結構風險最小化原理的支持向量機（SVM）相當的甚至更優的推廣性能，但其計算效率則遠優於SVM。正則判別分析法（CDA）尋找最優區分類別的坐標軸（k-1個正則坐標，k為類別的數量）。 這些線性函式是不相關的，實際上，它們通過n維數據云定義了一個最最佳化的k-1個空間，能夠最優的區分k個類（通過其在空間的投影）。。
多類LDA：當出現超過兩類的情況時，可以使用由費舍爾判別派生出的分析方法，它延伸為尋找一個保留了所有類的變化性的子空間。這是由 C.R.Rao 總結出來的。假設，C個類中每一個類都有均值和相同的協方差。
要實現典型的LDA技術前提是所有的樣本都必須提前準備完畢。但有些情況下，沒有現成的完整數據集或者輸入觀察數據是流的形式。這樣，就要求LDA的特徵提取有能力隨著觀察新樣本的增加而更新LDA的特徵，而不是在整個數據集上運行算法。例如，在移動機器人或實時臉部識別等實時套用中，提取的LDA特徵能隨著新觀察值實時更新是非常重要的。這種能夠通過簡單觀察新樣本來更新LDA特徵的技術就叫做增量LDA算法，在過去二十年里，它已經被廣泛的研究過。Catterjee和Roychowdhury提出了一種增量自組織LDA算法來更新LDA特徵。另外，Demir和Ozmehmet提出利用誤差改正和赫布學習規則的線上本地學習算法來更新LDA特徵。最後，Aliyari等人提供了快速增量LDA算法。
套用領域
破產預測
在基於財務比率和其他金融變數的破產預測中，LDA是第一個用來系統解釋公司進入破產或存活的統計學工具。儘管受到財務比率不遵守LDA常態分配假設的限制，Edward Altman的1968年模型仍然是實際套用的領先者。
臉部識別
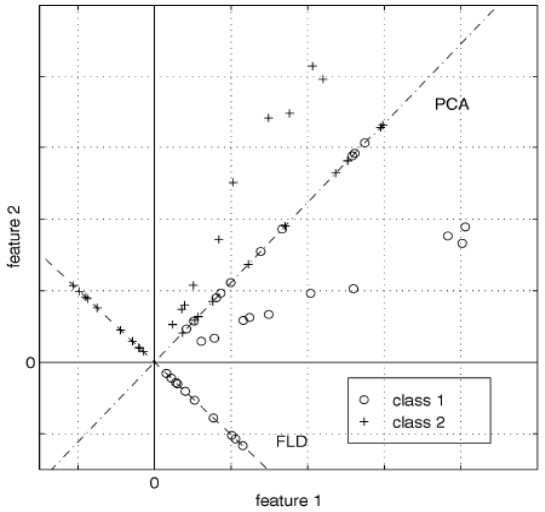
在計算機化的臉部識別中，每一張臉由大量像素值表達。 LDA在這裡的主要作用是把特徵的數量降到可管理的數量後再進行分類。每一個新的維度都是模板里像素值的線性組合。使用費舍爾線性判別得到的線性組合稱為費舍爾臉，而通過主成分分析（PCA）得到稱為特徵臉。
市場行銷
在市場行銷，判別分析曾經常用於通過市場調查或其他數據收集手段，找出那些能區分不同客戶或產品類型的多個因素。如今用的更多的是邏輯回歸或其他方法。在市場行銷中使用判別分析的具體步驟如下描述：
制定問題並收集數據 -- 識別消費者評估產品的一些顯著屬性 一 用定量市場研究技術（例如市場調查）從潛在消費者中收集關於他們對產品所有屬性的評分數據。數據收集階段通常是由專業的市場調查公司完成的。調查人員選擇一系列屬性，請參與者對他們給出1到5（或者1到7，1到10）的評分。通常選5到20個屬性。通常包括：易用度，重量，準確度，耐用性，色彩度，價格，或尺寸。根據研究的產品選擇不同的屬性。在調查中對所有的產品都問相同的問題。多個產品的數據編碼後，輸入統計分析程式，比如R，SPSS或SAS。。
估計的判別函式的係數並確定統計顯著水平和有效性 -- 選擇適當的判別分析方法。直接的方法涉及估計判別函式，以便所有的預測器同時被評估。逐步的方法順序進入的預測器。當因變數只有兩類或狀態時，適用兩組的方法。因變數多於三個是，用多類判別方法。在SPSS或者SAS里的F統計包，用Wilks's Lambda檢驗顯著水平。最常用的有效性檢驗方法是，將樣本分為兩組：估計/分析樣本和驗證樣本。估計樣本用來構建判別函式，驗證樣本構建分類矩陣，其中包括正確分類和不正確分類的數量。正確分類案例的百分比稱為命中率。將結果畫在二維圖裡，定義維度，並解釋結果。統計程式（或相關模組）會將結果做出圖。圖中包括每個產品（通常為二維空間）。每個產品之間的距離表明他們不同的程度。研究者必須給每個維度註明標籤。整個過程需要主觀判斷，非常具有挑戰性。。
生物醫學研究
判別分析在醫學的主要套用是評估患者的嚴重程度和對疾病結果的預後判斷。比如，在回顧分析中，根據患者的病情分為幾組：輕微，中度和嚴重。通過對臨床和實驗室分析結果的研究，揭示被研究組中哪些變數是統計上不同的。使用這些變數建立判別函式，幫助將未來的患者客觀的劃分到輕微，中度和嚴重的類別里。在生物學中，類似的原則被用以劃分和定義不同的生物對象。例如，用傅立葉變換紅外光譜定義沙門氏菌的噬菌體類別 檢測大腸桿菌的動物來源以研究它的毒力因子等。
地球科學
這種方法可用於區分蝕變帶。例如，當很多帶的不同數據都現成時，判別分析可以從數據中找到模式並有效的對它分類。
