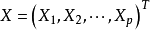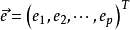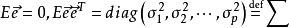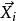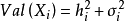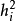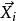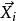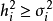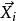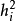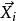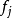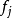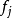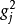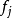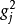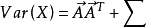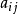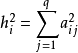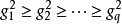因子分析是指研究從變數群中提取共性因子的統計技術。最早由英國心理學家C.E.斯皮爾曼提出。他發現學生的各科成績之間存在著一定的相關性，一科成績好的學生，往往其他各科成績也比較好，從而推想是否存在某些潛在的共性因子，或稱某些一般智力條件影響著學生的學習成績。因子分析可在許多變數中找出隱藏的具有代表性的因子。將相同本質的變數歸入一個因子，可減少變數的數目，還可檢驗變數間關係的假設。
基本介紹
- 中文名：因子分析
- 外文名：factor analysis
- 研究：變數群中提取共性因子
- 提出人：C.E.斯皮爾曼
- 方法：重心法、影像分析法等
- 學科：統計學
- 主成分分析：基礎的反覆法
簡介,隱性變數,得到因子,驗證因子,分析描述,因子套用,
簡介
且
,e的分量
稱為特殊因子，它僅對X的分量
起作用。
μ和A為參數矩陣。若X滿足上式，則稱隨機向量X具有因子結構。這時，容易算得
另一方面，對一個指定的公共因子 ，記
，稱為公共因子 對X的貢獻。
的值越大，反映了公共因子 對X的影響也越大，所以是衡量公共因子重要性的一個尺度。
隱性變數
因子分析的主要目的是用來描述隱藏在一組測量到的變數中的一些更基本的，但又無法直接測量到的隱性變數 (latent variable, latent factor)。比如，如果要測量學生的學習積極性(motivation)，課堂中的積極參與，作業完成情況，以及課外閱讀時間可以用來反應積極性。而學習成績可以用期中，期末成績來反應。在這裡，學習積極性與學習成績是無法直接用一個測度(比如一個問題) 測準，它們必須用一組測度方法來測量，然後把測量結果結合起來，才能更準確地把握。換句話說，這些變數無法直接測量。可以直接測量的可能只是它所反映的一個表征(manifest)，或者是它的一部分。在這裡，表征與部分是兩個不同的概念。表征是由這個隱性變數直接決定的。隱性變數是因，而表征是果，比如學習積極性是課堂參與程度 (表征測度)的一個主要決定因素。
因子分析是社會研究的一種有力工具，但不能肯定地說一項研究中含有幾個因子，當研究中選擇的變數變化時，因子的數量也要變化。此外對每個因子實際含意的解釋也不是絕對的。
得到因子
因子分析的方法有兩類。一類是探索性因子分析法，另一類是驗證性因子分析。探索性因子分析不事先假定因子與測度項之間的關係，而讓數據“自己說話”。主成分分析和共因子分析是其中的典型方法。驗證性因子分析假定因子與測度項的關係是部分知道的，即哪個測度項對應於哪個因子，雖然我們尚且不知道具體的係數。
驗證因子
探索的因子分析有一些局限性。第一，它假定所有的因子(旋轉後) 都會影響測度項。在實際研究中，我們往往會假定一個因子之間沒有因果關係，所以可能不會影響另外一個因子的測度項。第二，探索性因子分析假定測度項殘差之間是相互獨立的。實際上，測度項的殘差之間可以因為單一方法偏差、子因子等因素而相關。第三，探索性因子分析強制所有的因子為獨立的。這雖然是求解因子個數時不得不採用的機宜之計，卻與大部分的研究模型不符。最明顯的是，自變數與應變數之間是應該相關的，而不是獨立的。這些局限性就要求有一種更加靈活的建模方法，使研究者不但可以更細緻地描述測度項與因子之間的關係，而且可以對這個關係直接進行測試。而在探索性因子分析中，一個被測試的模型(比如正交的因子) 往往不是研究者理論中的確切的模型。
分析描述
驗證性因子分析(confirmatory factor analysis) 的強項正是在於它允許研究者明確描述一個理論模型中的細節。那么一個研究者想描述什麼呢？我們曾經提到因為測量誤差的存在，研究者需要使用多個測度項。當使用多個測度項之後，我們就有測度項的“質量”問題，即有效性檢驗。而有效性檢驗就是要看一個測度項是否與其所設計的因子有顯著的載荷，並與其不相干的因子沒有顯著的載荷。當然，我們可能進一步檢驗一個測度項工具中是否存在單一方法偏差，一些測度項之間是否存在“子因子”。這些測試都要求研究者明確描述測度項、因子、殘差之間的關係。對這種關係的描述又叫測度模型 (measurement model)。對測度模型的質量檢驗是假設檢驗之前的必要步驟。
因子套用
在市場調研中，研究人員關心的是一些研究指標的集成或者組合，這些概念通常是通過等級評分問題來測量的，如利用李克特量表取得的變數。每一個指標的集合（或一組相關聯的指標）就是一個因子，指標概念等級得分就是因子得分。
因子分析在市場調研中有著廣泛的套用，主要包括：
（1）消費者習慣和態度研究（U&A）
（2） 品牌形象和特性研究
（3）服務質量調查
（4） 個性測試
（5）形象調查
（6） 市場劃分識別
（7）顧客、產品和行為分類
在實際套用中，通過因子得分可以得出不同因子的重要性指標，而管理者則可根據這些指標的重要性來決定首先要解決的市場問題或產品問題。
