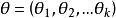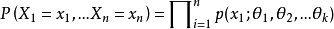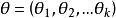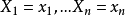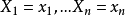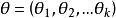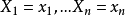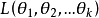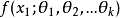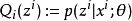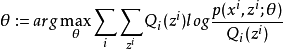定義
最大似然估計,只是一種機率論在統計學的套用,它是參數估計的方法之一。說的是已知某個隨機樣本滿足某種機率分布,但是其中具體的參數不清楚,參數估計就是通過若干次試驗,觀察其結果,利用結果推出參數的大概值。最大似然估計是建立在這樣的思想上:已知某個參數能使這個樣本出現的機率最大,我們當然不會再去選擇其他小機率的樣本,所以乾脆就把這個參數作為估計的真實值。
離散型
設X為離散型隨機變數,
為多維參數向量,如果隨機變數相互獨立,則可得機率函式
,在
固定時,上式表示
的機率;當
已知的時候,它又變成
的函式,可以把它記為
,稱此函式為似然函式。似然函式值的大小意味著該樣本值出現的可能性的大小,既然已經得到了樣本值
,那么它出現的可能性應該是較大的,即似然函式的值也應該是比較大的,因而最大似然估計就是選擇使
達到最大值的那個
作為真實的估計。
連續型
設X為連續型隨機變數,其機率密度函式為
,
為從該總體中抽出的樣本,同樣的如果相互獨立且同分布,於是樣本的聯合機率密度為
。大致過程同離散型一樣。
求解步驟
(1) 寫出似然函式
(2) 對似然函式取對數,並整理
(3) 求導數
(4) 解似然方程
用途
參數估計
根據從總體中抽取的樣本估計總體分布中包含的未知參數的方法。它是統計推斷的一種基本形式,是數理統計學的一個重要分支,分為點估計和區間估計兩部分。
點估計:依據樣本估計總體分布中所含的未知參數或未知參數的函式。 常用方法有:矩估計法、極大似然估計法、最小二乘法、貝葉斯估計法。
區間估計(置信區間的估計):依據抽取的樣本,根據一定的正確度與精確度的要求,構造出適當的區間,作為總體分布的未知參數或參數的函式的真值所在範圍的估計。例如人們常說的有百分之多少的把握保證某值在某個範圍內,即是區間估計的最簡單的套用。
套用
1.樸素貝葉斯法
在常態分配前提下求出了p時刻預測值yp的先驗分布密度和後驗分布密度,由已知的信息估計了兩個協方差陣。最後求出yp的貝葉斯極大似然估計,它是兩個組合預測的加權平均,本身仍為一組合預測,其權重隨預測時刻p的改變而改變。
2.EM算法
利用傳統的估計方法確定混合常態分配參數極大似然估計是很困難的.為此採用EM統計算法,引入恰當的"潛在數據"簡化了計算過程,將複雜的極大化運算轉化為一系列求期望和極大化的簡單步驟.算例結果表明EM算法是有效的,估值精度滿足要求.
期望最大算法是一種從不完全數據或有數據丟失的數據集(存在隱含變數)中求解機率模型參數的最大似然估計方法。
EM的算法流程:
初始化分布參數θ;
重複以下步驟直到收斂:
E步驟:根據參數初始值或上一次疊代的模型參數來計算出隱性變數的後驗機率,其實就是隱性變數的期望。作為隱藏變數的現估計值:
M步驟:將似然函式最大化以獲得新的參數值:
這個不斷的疊代,就可以得到使似然函式L(θ)最大化的參數θ了。