對數似然方程(log-likelihood equation)亦簡稱“似然方程”。對數似然方程與原似然方程同解,由於獨立同分布的樣本的似然函式上具有連乘積,對似然方程取對數更方便計算。
基本介紹
- 中文名:對數似然方程
- 外文名:log-likelihood equation
- 簡稱:似然方程
- 所屬學科:數學
- 所屬問題:統計學(估計方法)
基本概念
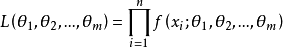
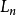
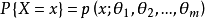
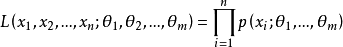
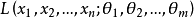


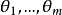
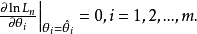



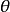
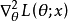

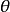


例題解析
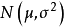
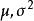

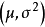

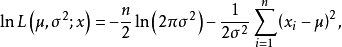

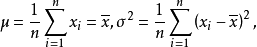
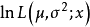
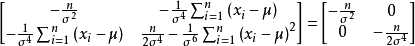
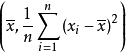
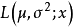
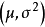
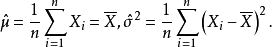

對數似然方程(log-likelihood equation)亦簡稱“似然方程”。對數似然方程與原似然方程同解,由於獨立同分布的樣本的似然函式上具有連乘積,對似然方程取對數更方便計算。
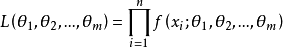
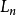
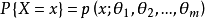
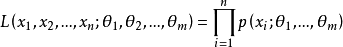
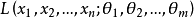


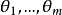
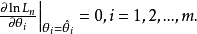



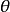
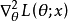

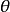


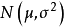
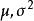

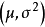

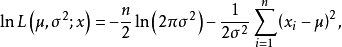

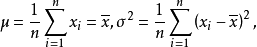
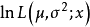
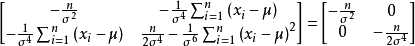
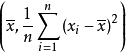
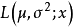
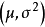
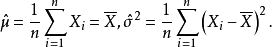
對數似然方程(log-likelihood equation)亦簡稱“似然方程”。對數似然方程與原似然方程同解,由於獨立同分布的樣本的似然函式上具有連乘積,對似然方程取對數更方便計算...
涉及到似然函式的許多套用中,更方便的是使用似然函式的自然對數形式,即“對數似然函式”。求解一個函式的極大化往往需要求解該函式的關於未知參數的偏導數。由於對數...
1.求極大似然函式估計值的一般步驟:(1) 寫出似然函式;(2) 對似然函式取對數,並整理;(3) 求導數;(4) 解似然方程 。2.利用高等數學中求多元函式的極值的...
解對數似然方程所得,即為未知參數 的最大似然估計值。 [1] 最大似然估計例題 編輯 設總體X~N(μ,σ2),μ,σ為未知參數,X1,X2...,Xn是來自總體X的樣本...
通過解方程dL(θ)/dθ=0來得到,因為lnL(θ)和L(θ)的增減性相同,所以它們在θ的同一值處取得最大值,稱lnL(θ)為對數似然函式,可以通過求解對數似然函式的...
(1) 寫出似然函式(2) 對似然函式取對數,並整理(3) 求導數(4) 解似然方程極大似然估計法用途 編輯 參數估計根據從總體中抽取的樣本估計總體分布中包含的未知...
要求θ的最大似然估計 ,必需解似然方程:由於對數函式的單調性,取對數似然函式進行估計,則有:此式為必要條件,而不是充分條件。例5.1 在假設H1和H0下,接收信號...
泊松回歸假設反應變數Y是泊松分布,並假設它期望值的對數可被未知參數的線性組合...為了找到極大值,需要求解方程: 可以通過對其似然函式取負值 (negative log-...
