連續型隨機變數是指如果隨機變數X的所有可能取值不可以逐個列舉出來,而是取數軸上某一區間內的任一點的隨機變數。例如,一批電子元件的壽命、實際中常遇到的測量誤差等都是連續型隨機變數。
基本介紹
- 中文名:連續型隨機變數
- 外文名:Continuous random variable
- 領域:數學
- 類別:數學概念
數學定義
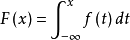
- 若f(x)在點x連續,則有F’(x)=f(x)
- f(x)是可積,則它的原函式F(x)連續;
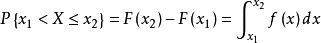


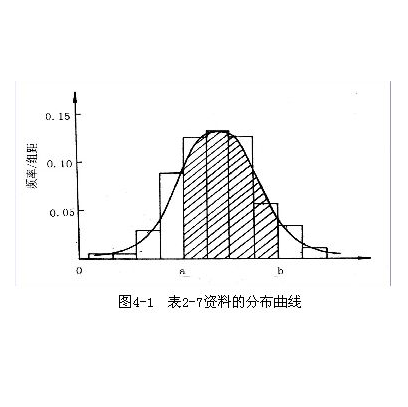
連續型隨機變數是指如果隨機變數X的所有可能取值不可以逐個列舉出來,而是取數軸上某一區間內的任一點的隨機變數。例如,一批電子元件的壽命、實際中常遇到的測量誤差等都是連續型隨機變數。
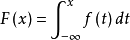
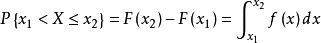


連續型隨機變數是指如果隨機變數X的所有可能取值不可以逐個列舉出來,而是取數軸上某一區間內的任一點的隨機變數。例如,一批電子元件的壽命、實際中常遇到的測量誤差...
連續性隨機變數X的分布函式F(x)可表示成一個非負可積函式f(x)的積分,則稱X為連續性隨機變數,f(x)稱為X的機率密度函式(分布密度函式)。能按一定次序一一...
隨機變數(random variable)表示隨機試驗各種結果的實值單值函式。隨機事件不論與數量是否直接有關,都可以數量化,即都能用數量化的方式表達。隨機事件數量化的好處是...
連續型分布(continuous distribution)隨機變數的兩個常用的分布類型之一。...... 連續型分布(continuous distribution)隨機變數的兩個常用的分布類型之一。...
在數學上,利用測度論可定義隨機過程如下:設給定參數集合T和可測空間(E,B).若對每一t∈T,有一個定義在機率空間(Ω,F,P)上的E值B可測函式(即隨機變數)X...
獨立隨機變數是機率論的基本概念之一。稱隨機變數X,…,Y為相互獨立的,如果它們的聯合分布函式等於各個變數的分布函式的乘積。連續型隨機變數X,…,Y相互獨立,當且...
連續型均勻分布,如果連續型隨機變數具有某種特定的機率密度函式,則稱X服從[A,B]上的均勻分布(uniform distribution)。...
隨機量,即隨機變數(random variable)表示隨機試驗各種結果的實值單值函式。隨機事件不論與數量是否直接有關,都可以數量化,即都能用數量化的方式表達。...
連續分布( continuous distribution)連續型隨機變數X的分布函式是連續的,它對應的分布為連續分布。常用的連續分布有常態分配、均勻分布、指數分布、伽瑪分布、貝塔分布...
在機率論和統計學中,數學期望(mean)(或均值,亦簡稱期望)是試驗中每次可能結果的機率乘以其結果的總和,是最基本的數學特徵之一。它反映隨機變數平均取值的大小。...
在數學中,連續型隨機變數的機率密度函式(在不至於混淆時可以簡稱為密度函式)是一個描述這個隨機變數的輸出值,在某個確定的取值點附近的可能性的函式。而隨機變數的...
分布函式(英文Cumulative Distribution Function, 簡稱CDF),是機率統計中重要的函式,正是通過它,可用數學分析的方法來研究隨機變數。分布函式是隨機變數最重要的機率...
總體均值(population mean)又叫做總體的數學期望或簡稱期望,是描述隨機變數取值平均狀況的數字特徵。包括離散型隨機變數的總體均值:和連續型隨機變數的總體均值。...
機率分布函式是機率論的基本概念之一。在實際問題中,常常要研究一個隨機變數ξ取值小於某一數值x的機率,這機率是x的函式,稱這種函式為隨機變數ξ的分布函式,簡稱...
類似地,對連續隨機變數而言,聯合分布機率密度函式為fX,Y(x, y),其中fY|X(y|x)和fX|Y(x|y)分別代表X = x時Y的條件分布以及Y = y時X的條件分布;fX(...
累積機率分布,又稱累積分布函式、分布函式等,用於描述隨機變數落在任一區間上的機率,常被視為數據的某種特徵。若該變數是連續變數,則累積機率分布是由機率密度函式...
(variance)是在機率論和統計方差衡量隨機變數或一組數據時離散程度的度量。機率論中方差用來度量隨機變數和其數學期望(即均值)之間的偏離程度。統計中的方差(樣本...
常態分配具有兩個參數μ和σ^2的連續型隨機變數的分布,第一參數μ是服從常態分配的隨機變數的均值,第二個參數σ^2是此隨機變數的方差,所以常態分配記作N(μ,...
