基本介紹
- 中文名:隨機量
- 外文名:random variable
- 領域:數學
- 別稱:隨機變數
定義
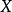
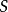

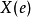

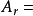
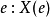
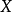
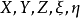
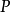
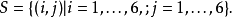
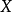
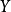
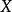
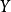
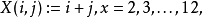
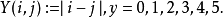
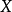
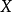
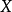
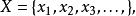
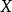
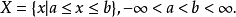
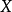

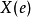

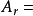
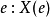
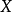
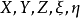
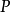
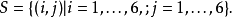
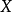
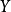
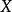
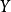
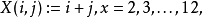
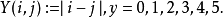
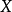
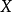
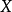
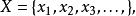
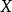
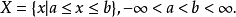
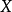
隨機量,即隨機變數(random variable)表示隨機試驗各種結果的實值單值函式。隨機事件不論與數量是否直接有關,都可以數量化,即都能用數量化的方式表達。...
隨機測量:主要是對各種噪聲信號進行動態測量和統計分析。 ...... 隨機測量:主要是對各種噪聲信號進行動態測量和統計分析。V百科往期回顧 詞條統計 瀏覽次數:次 編輯...
隨機向量由多個隨機變數組成的向量。...... 隨機向量[1] (random vector)由多個隨機變數組成的向量。給定樣本空間,如果其上的實值函式 是 (實值)可測函式,則...
中央隨機(center random)是指在科學研究中為了實現盲法,排除人為或者其它未知因素對研究結果產生偏差影響而採用的一種有計算機系統中央控制動態區組隨機方法來實現的一...
隨機向量分布函式(distribution function ofrandom vector)能完全描述隨機向量機率分布的多元函式。...
隨機遊走(random walk)也稱隨機漫步,隨機行走等是指基於過去的表現,無法預測將來的發展步驟和方向。核心概念是指任何無規則行走者所帶的守恆量都各自對應著一個擴散...
獨立隨機向t(independent random vectors )一類重要的隨機向量。...... 獨立隨機向t(independent random vectors )一類重要的隨機向量。指隨機向量相互之間具有獨立性....
連續型隨機向量(absolutly continuous randomvector)一類重要的隨機向量。...... 連續型隨機向量(absolutly continuous randomvector)一類重要的隨機向量。...
離散型隨機向量(discrete random vector)類重要的隨機向量。...... 離散型隨機向量(discrete random vector)類重要的隨機向量。如果n維隨機向量濘_峪1,之... ,)最...
二維隨機向量亦稱二維隨機變數,是機率論的基本概念之一,屬於數學名詞。...... 二維隨機向量亦稱二維隨機變數,是機率論的基本概念之一,屬於數學名詞。二維隨機向量(two...
隨機向量獨立性檢驗( test of independence ofrandom vector)具有聯合常態分配的m(m≥2)個隨機向量之間的獨立性檢驗。 ...
協因數(矩)陣(cofactor matrix)隨機向量精度的表示方法之一它是由一個隨機向量中各元素的協因數和兩兩元素之間的互協因數按一定順序排列而成的矩陣.例如,設有((...
常態分配具有兩個參數μ和σ^2的連續型隨機變數的分布,第一參數μ是服從常態分配的隨機變數的均值,第二個參數σ^2是此隨機變數的方差,所以常態分配記作N(μ,...
經典測量理論亦稱“真分數理論”。2O 世紀初提出,至 50 年代臻於完善。該理論假設觀測分數 X 是由真分數 T 及隨機測量誤差 E 所組成,即 X= T+ E;誤差 E...
設x1, x2,..., xN為隨機變數x的獨立同分布的N個觀測樣值,p(x|θ)為x的依賴參量θ分布密度函式,參量θ為待估計的量。則似然函式如圖12: 圖12 ...
1.1直接測量:在測量過程中,能夠直接將被測量與同類標準量進行比較,或能夠直接用...3.4隨機測量:隨機測量又叫做統計測量,主要是對各類噪聲信號進行動態測量和統計分...
它代表每秒或每個信道符號能傳送的最大信息量,或者說小於這個數的信息率必能在...信道的輸入、輸出都取值於離散符號集,且都用一個隨機變數來表示的信道就是離散...
所謂計量經濟模型,就是表示經濟現象及其主要因素之間數量 關係的方程式。計量經濟模型主要有經濟變數、參數以及隨機誤差三大要素。經濟變數是反映經濟 變動情況的量,分...
因子自由度(Factor degree of freedom)在統計數據中指統計量在最終計算中可隨意變化的數值。自由度的數量定義為可完全指定系統位置的獨立坐標的最小值。在數學上,...
使p(Y*θ)最大的θ就是極大似然估計量,通常用表示。估計理論貝葉斯估計 對於單參量估計(多參量估計的情況相似)來說,首先要給定隨機參量 θ的機率密度函式p(θ...
本書系統論述了大規模網路下認知測量的基本理論及某些套用問題,基本涵蓋了認知測量在理論和實際套用中各個方面的內容。全書包括隨機矩陣和的性質,隨機矩陣的集中不...
1 歷史 2 特點 3 標準 4 電信測量分類 5 隨機測量技術 6 電信測量儀器分類 電信測量歷史 20世紀70年代以來,由於電信技術、電子計算機技術和積體電路的迅...
編輯 本書內容包括初等機率計算、隨機變數及其分布、數字特徵、多維隨機向量、極限定理、統計學基本概念、點估計與區間估計、假設檢驗、回歸相關分析、方差分析等。書...
