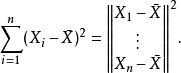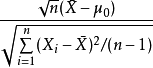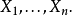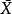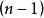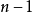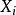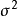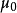因子自由度

因子自由度（Factor degree of freedom）在統計數據中指統計量在最終計算中可隨意變化的數值。自由度的數量定義為可完全指定系統位置的獨立坐標的最小值。在數學上，自由度是隨機向量域的維數，或者基本上是“自由”分量的數量。該術語最常用於線性模型（線性回歸、方差分析）背景下，在某些隨機向量被約束在線性子空間中，自由度數量是子空間的維數。

基本介紹

• 中文名：因子自由度
• 外文名：Factor degree of freedom
• 學科：統計學

簡介

在統計數據中，因子自由度是統計量最終計算中可以隨意變化的數值。動態系統可以移動的獨立方式的數量不會違反強加給它的任何約束，稱為自由度。換句話說，自由度的數量可以定義為可以完全指定系統位置的獨立坐標的最小數量。統計參數的估計可以基於不同量的信息或數，進入參數估計的獨立信息的數量稱為自由度。

在數學上，自由度是隨機向量的域的維數，或者基本上是“自由”分量的數量（在完全確定向量之前需要知道多少組件）。

該術語最常用於線性模型（線性回歸、方差分析）的背景下，其中某些隨機向量被約束在線性子空間中，並且自由度的數量是子空間的維數。自由度通常還與這些矢量的平方長度（或坐標的“平方和”）以及在相關統計測試問題中出現的卡方分布或其他分布參數相關聯。

雖然介紹性教科書可能會將因子自由度作為分布參數或通過假設檢驗引入，它是定義自由度的基礎幾何，對於正確理解這一概念至關重要。

符號

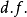在等式中，自由度的典型符號是 。在文本和表格中，通常使用縮寫“ ”。RA Fisher曾用 表示自由度，但現在通常用 表示樣本量

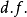
隨機向量

在幾何學上，因子自由度可以解釋為某些向量子空間的維數。作為一個起點，假設我們有一個獨立常態分配觀測樣本： 這可以表示為一個 維隨機向量：

由於這個隨機向量可以位於維空間的任何地方，因此它具有個自由度。

現在，讓我們 是樣本的意思。隨機向量可以分解為樣本均值加殘差向量之和：

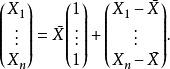
右側的第一個向量被限制為1的向量的倍數，並且唯一的自由量是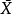 。因此它有1個自由度。

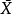
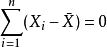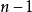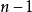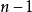第二個向量受關係限制 。這個矢量的第一個 分量可以任意選擇。但是，一旦知道了前 個組件，該約束就會告訴您第 個組件的值。因此，這個矢量具有 個自由度。

在數學上，第一個向量是數據向量在1自由度的向量跨越子空間上的正交或最小二乘投影。1自由度是這個子空間的維度。第二個殘差向量是該子空間 維正交補數上的最小二乘投影，具有 個自由度。

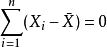
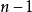
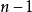
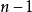
在統計測試套用中，通常一個人對組件向量沒有直接感興趣，而是對它們的平方長度感興趣。在上面的例子中，殘差平方和是

如果數據點以均值0和方差分布 ，那么剩餘的平方和具有縮放的卡方分布（按因子縮放），個自由度。因子自由度（這裡是分布的參數）仍然可以被解釋為底層矢量子空間的維度。

同樣，單樣本t檢驗統計量，

當假設均值時，遵循學生t分布，自由度是正確的。同樣，自由度來自分母中的殘差向量。