基本介紹
- 中文名:分布參數
- 外文名:Distribution parameters
- 相關概念:參數空間
- 舉例:總體均值、標準差、相關係數
- 領域:統計學
- 學科:數學
定義
類型

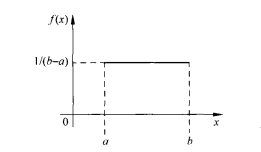 圖1均勻分布U(a,b)的密度函式
圖1均勻分布U(a,b)的密度函式
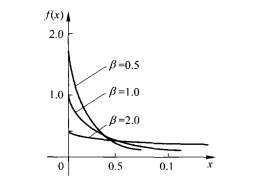 圖2 指數函式Exp(β)的密度函式
圖2 指數函式Exp(β)的密度函式
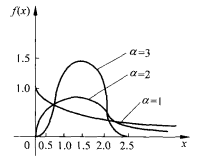 圖3韋伯分布Weibull(α,β)的密度函式
圖3韋伯分布Weibull(α,β)的密度函式估計




舉例



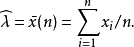

 圖1均勻分布U(a,b)的密度函式
圖1均勻分布U(a,b)的密度函式
 圖2 指數函式Exp(β)的密度函式
圖2 指數函式Exp(β)的密度函式
 圖3韋伯分布Weibull(α,β)的密度函式
圖3韋伯分布Weibull(α,β)的密度函式





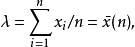

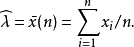
分布參數(distributed parameter)是統計學的基本概念之一。指統計學中用以區別分布函式族{Fθ|θ∈Θ}中的各個分布的指標θ的函式g(θ)和分布的數字特徵,如總體...
分布參數電路是指在高頻工作下,傳輸線的分布參數效應不能被忽略,其電氣特性由單位線長上的分布電感、分布電容、分布電阻和分布電導來描述,這時傳輸線已與串聯電感和...
分布參數控制系統(distributed parameter con-trol system)含控制作用的分布參數系統。泛指用分布參數系統描述的受控對象的控制,控制的目的是改變系統的性能品質,以適合...
分布參數系統開放分類:數學術語術語科學自然科學 編輯詞條分享 狀態變化不能只用有限個參數而必須用場(一維或多維空間變數的函式)來描述的系統。在實際問題中,參數的...
分布參數系統,是為集中參數系統或集總參數系統中的一種情況。分布參數系統的典型實例有:電磁場、引力場、溫度場等物理場,彈性梁型的運動體,大型加熱爐,水輪機和...
學科:水文地質學 詞目:分布參數模型 英文:distributed parameter model 釋文:描述系統特徵、動態隨空間坐標變化的模型,通常是指由流體力學定律和原理導出的多孔介質中...
機率與統計相關學科中,愛爾朗分布(Erlang Distribution)是一種連續型機率分布。Erlang分布的譯名較多,如愛爾蘭分布,埃朗分布,埃爾朗分布,愛爾朗分布,厄朗分布等等;此外...
分布參數測量儀表,測量微波元件和微波網路參數測量儀。常用來測量反射係數或駐波比、阻抗、傳輸常數、散射參數等。 ...
參數控制,是指對變數系統實現的控制。指內在含量。例如:橡膠配方等。...... 高超聲速發動機表現出了明顯的分布參數特性,採用集中參數控制方法難以滿足發動機控制要求。...
《動態分布參數的貝葉斯可靠性分析》是2011年國防工業出版社出版的圖書,作者是明志茂。本書主要介紹了動態分布參數的貝葉斯可靠性分析專業知識。...
它是總體分布參數θ的一個機率分布。貝葉斯學派的根本觀點,是認為在關於θ的任何統計推斷問題中,除了使用樣本X所提供的信息外,還必須對θ規定一個先驗分布,它是在...
玻爾茲曼分布也叫吉布斯分布,是一種覆蓋系統各種狀態的機率分布、機率測量或者頻率分布。當有保守外力(如重力場、電場等)作用時,氣體分子的空間位置就不再均勻分布了...
