基本介紹
- 中文名:先驗分布
- 外文名:prior distribution
- 適用範圍:數理科學
定義
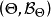
描述
後驗分布
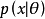
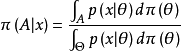
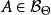

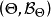
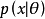
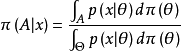
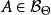
先驗分布(prior distribution)一譯“驗前分布”“事前分布”。是機率分布的一種。與“後驗分布”相對。與試驗結果無關,或與隨機抽樣無關,反映在進行統計試驗之前...
先驗機率(prior probability)是指根據以往經驗和分析得到的機率,如全機率公式,它往往作為"由因求果"問題中的"因"出現的機率。在貝葉斯統計推斷中,不確定數量的先驗...
貝塔分布(Beta Distribution) 是一個作為伯努利分布和二項式分布的共軛先驗分布的密度函式,在機器學習和數理統計學中有重要套用。在機率論中,貝塔分布,也稱Β分布,是...
共轆先驗分布族(conjugate prior distributionfamily)具有共扼性質的先驗分布族.有時將共扼性作為選擇先驗分布族的原則.給定統計結構(眯,,必,,),如果夕中的機率...
逆威沙特分布,也叫反威沙特分布,是統計學中出現的一類機率分布函式,定義在實值的正定矩陣上。...
它是總體分布參數θ的一個機率分布。貝葉斯學派的根本觀點,是認為在關於θ的任何統計推斷問題中,除了使用樣本X所提供的信息外,還必須對θ規定一個先驗分布,它是在...
貝葉斯方法是基於貝葉斯定理而發展起來用於系統地闡述和解決統計問題的方法。一個完全的貝葉斯分析包括數據分析、機率模型的構造、先驗信息和效應函式的假設以及最後的...
貝葉斯估計(Bayesian estimation)是利用貝葉斯定理結合新的證據及以前的先驗機率,來得到新的機率。它提供了一種計算假設機率的方法,基於假設的先驗機率、給定假設下觀察...
當先驗分布未知時,利用歷史樣本來估計先驗分布,並確定貝葉斯決策函式,這樣的方法稱為經驗貝葉斯方法。一個決策函式,它不僅利用當前樣本,還利用歷史本來確定先驗分布,稱...
貝葉斯學習是利用參數的先驗分布,由樣本信息求來的後驗分布,直接求出總體分布。貝葉斯學習理論使用機率去表示所有形式的不確定性,通過機率規則來實現學習和推理過程。...
客觀貝葉斯方法(或是不提供信息的貝葉斯方法)中,統計分析只依照假設的模型、分析的資料以及給定先驗分布的方式(不同的客觀貝葉斯方法會有不同給定先驗分布的方式)。...
我們可以看到使用先驗分布,把θj當作一個總體分布的樣本是很自然的事情。這樣的套用有一個很關鍵的點是,觀測數據,yij,其中 i 表示組的索引,j 表示單元的索引,...
貝葉斯預測是一種以動態模型為研究對象的時間序列預測方法,一般模式為先驗+總體分布+樣本→後驗分布。...
本書系統地介紹了貝葉斯統計的基本思想及其來龍去脈、先驗分布和後驗分布的概念以及尋求方法、貝葉斯統計推斷、MCMC計算方法以及統計決策理論等。為使初學者更好地...
1.對每一項活動,輸入最小、最大和最可能估計數據,並為其選擇一種合適的先驗分布模型;2.計算機根據上述輸入,利用給定的某種規則,快速實施充分大量的隨機抽樣3.對...
貝葉斯分析方法(Bayesian Analysis)是貝葉斯學習的基礎,它提供了一種計算假設機率的方法,這種方法是基於假設的先驗機率、給定假設下觀察到不同數據的機率以及觀察到的...
