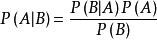當先驗分布未知時,利用歷史樣本來估計先驗分布,並確定貝葉斯決策函式,這樣的方法稱為經驗貝葉斯方法。一個決策函式,它不僅利用當前樣本,還利用歷史本來確定先驗分布,稱這樣的決策函式為經驗貝葉斯決策函式。
基本介紹
- 中文名:經驗貝葉斯方法
- 外文名:empirical Bayes method
- 適用範圍:數理科學
定義,分類,貝葉斯定理,
定義
當先驗分布未知時,利用歷史樣本來估計先驗分布,並確定貝葉斯決策函式,這樣的方法稱為經驗貝葉斯方法。一個決策函式,它不僅利用當前樣本,還利用歷史本來確定先驗分布,稱這樣的決策函式為經驗貝葉斯決策函式。
分類
經驗貝葉斯方法通常可分為參數經驗貝葉斯方法和非參數經驗貝葉斯方法兩種。
設樣本的條件密度為 ,參數
,參數 的先驗分布
的先驗分布 未知。記樣本的邊緣密度為
未知。記樣本的邊緣密度為



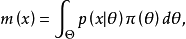
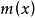
若假設 的先驗分布屬於一己知的參數族,記為
的先驗分布屬於一己知的參數族,記為 ,則樣本的邊緣密度可寫為
,則樣本的邊緣密度可寫為 。那么,基於獨立同分布
。那么,基於獨立同分布 的歷史樣本
的歷史樣本 ,利用經典統計方法可以給出λ 的估計
,利用經典統計方法可以給出λ 的估計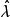 ,進而得到先驗分布的估計
,進而得到先驗分布的估計 ,並以其貝葉斯解為經驗貝葉斯決策函式。這種方法稱為參數經驗貝葉斯方法。
,並以其貝葉斯解為經驗貝葉斯決策函式。這種方法稱為參數經驗貝葉斯方法。





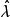

若決策問題的貝葉斯解可以表示為 ,其中
,其中 和
和 是已知的函式,則可以用服從
是已知的函式,則可以用服從 的獨立樣本來估計
的獨立樣本來估計 ,進而估計貝葉斯解
,進而估計貝葉斯解 並作為決策問題的經驗貝葉斯決策函式。這種方法稱為非參數經驗貝葉斯方法。
並作為決策問題的經驗貝葉斯決策函式。這種方法稱為非參數經驗貝葉斯方法。






經驗貝葉斯方法的關鍵是要有歷史樣本。
貝葉斯定理
在貝葉斯定理中,每個名詞都有約定俗成的名稱:
按這些術語,Bayes定理可表述為:
後驗機率 = (相似度*先驗機率)/標準化常量
也就是說,後驗機率與先驗機率和相似度的乘積成正比。
另外,比例P(B|A)/P(B)也有時被稱作標準相似度(standardised likelihood),Bayes定理可表述為:
後驗機率 = 標準相似度*先驗機率