貝葉斯學習是利用參數的先驗分布,由樣本信息求來的後驗分布,直接求出總體分布。貝葉斯學習理論使用機率去表示所有形式的不確定性,通過機率規則來實現學習和推理過程。
基本介紹
- 中文名:貝葉斯學習
- 外文名:Bayesian learning
- 結果表達:可理解為對不同可能性的信任程度
- 提出者:托馬斯.貝葉斯
- 含義分類:自動學習機制
- 相關衍伸:貝葉斯網路,貝葉斯推理
背景

貝葉斯定理
全機率公式





貝葉斯公式







貝葉斯定理




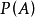






基本方法
生活套用




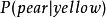


貝葉斯學習是利用參數的先驗分布,由樣本信息求來的後驗分布,直接求出總體分布。貝葉斯學習理論使用機率去表示所有形式的不確定性,通過機率規則來實現學習和推理過程。

















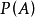










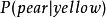


貝葉斯學習是利用參數的先驗分布,由樣本信息求來的後驗分布,直接求出總體分布。貝葉斯學習理論使用機率去表示所有形式的不確定性,通過機率規則來實現學習和推理過程。...
介紹貝葉斯學習是利用參數的先驗分布和由樣本信息求來的後驗分布,直接求出總體分布。 貝葉斯學習理論使用機率去表示所有形式的不確定性,通過機率規則來實現學習和推理...
貝葉斯法則(Bayes'theorem/Bayes theorem/Bayesian law) 貝葉斯的統計學中有一個基本的工具叫“貝葉斯法則”, 儘管它是一個數學公式,但其原理毋需數字也可明了。...
一般貝葉斯網路的構建是首先由相關領域的專家根據事物間的關係來確定出結構模型,即有向無環圖,然後再利用其它方法確定每個節點的條件機率,但這樣構建的網路模型無法...
貝葉斯分析方法(Bayesian Analysis)是貝葉斯學習的基礎,它提供了一種計算假設機率的方法,這種方法是基於假設的先驗機率、給定假設下觀察到不同數據的機率以及觀察到的...
貝葉斯(約1702-1761) Thomas Bayes,英國數學家。約1702年出生於倫敦,做過神甫。1742年成為英國皇家學會會員。1761年4月7日逝世。貝葉斯在數學方面主要研究機率論。...
貝葉斯分類算法是統計學的一種分類方法,它是一類利用機率統計知識進行分類的算法。在許多場合,樸素貝葉斯(Naïve Bayes,NB)分類算法可以與決策樹和神經網路分類算法...
貝葉斯決策理論是主觀貝葉斯派歸納理論的重要組成部分。 貝葉斯決策就是在不完全情報下,對部分未知的狀態用主觀機率估計,然後用貝葉斯公式對發生機率進行修正,最後再...
《貝葉斯思維統計建模的Python學習法》是人民郵政出版社出版的一部圖書。...... 《貝葉斯思維統計建模的Python學習法》是人民郵政出版社出版的一部圖書。...
貝葉斯分類器是各種分類器中分類錯誤機率最小或者在預先給定代價的情況下平均風險最小的分類器。它的設計方法是一種最基本的統計分類方法。其分類原理是通過某對象的...
結構學習是指貝葉斯網路結構學習。...... 由於貝葉斯網路結構學習是一個NP難問題,因此基於評分搜尋的貝葉斯網路結構學習方法中的搜尋算法一般採用啟發式搜尋算法。國內外...
貝葉斯網路(BN),又稱為信度網,由一個有向無環圖(Directed Acylic Graph,DAG)和條件機率表(ConditionalProbability Table,CPT)組成。...
貝葉斯推斷(英語:Bayesian inference)是推論統計的一種方法。這種方法使用貝葉斯定理,在有更多證據及信息時,更新特定假設的機率。貝葉斯推斷是統計學(特別是數理統計學...
《貝葉斯網路參數學習及對無人機的決策支持》是一部2012-11出版的圖書,頁數是152頁。...
貝葉斯估計(Bayesian estimation)是利用貝葉斯定理結合新的證據及以前的先驗機率,來得到新的機率。它提供了一種計算假設機率的方法,基於假設的先驗機率、給定假設下觀察...
貝葉斯線性回歸(Bayesian linear regression)是使用統計學中貝葉斯推斷(Bayesian inference)方法求解的線性回歸(linear regression)模型12。貝葉斯線性回歸將線性模型的參數...
貝葉斯定理是關於隨機事件A和B的條件機率(或邊緣機率)的一則定理。其中P(A|B)是在B發生的情況下A發生的可能性。貝葉斯定理也稱貝葉斯推理,早在18世紀,英國學者...
貝葉斯信息準則,也稱為Bayesian Information Criterion(BIC)貝葉斯決策理論是主觀貝葉斯派歸納理論的重要組成部分。是在不完全情報下,對部分未知的狀態用主觀機率估計,...
層次貝葉斯模型是具有結構化層次的統計模型。它可以用來為複雜的統計問題建立層次模型從而避免參數過多導致的過擬合問題。...
貝葉斯網路(Bayesian network),又稱信念網路(belief network)或是有向無環圖模型(directed acyclic graphical model),是一種機率圖型模型。...
樸素貝葉斯法是基於貝葉斯定理與特徵條件獨立假設的分類方法。最為廣泛的兩種分類模型是決策樹模型(Decision Tree Model)和樸素貝葉斯模型(Naive Bayesian Model,NBM)。...
