基本介紹
定義,性質,例子,特徵函式,套用,
定義
連續型隨機變數的機率密度函式有如下性質:
如果機率密度函式fX(x)在一點x上連續,那么累積分布函式可導,並且它的導數:

由於隨機變數X的取值 只取決於機率密度函式的積分,所以機率密度函式在個別點上的取值並不會影響隨機變數的表現。更準確來說,如果一個函式和X的機率密度函式取值不同的點只有有限個、可數無限個或者相對於整個實數軸來說測度為0(是一個零測集),那么這個函式也可以是X的機率密度函式。
性質
密度函式f(x) 具有下列性質:
① ;
;

② ;
;

③

例子

隨著參數μ和σ變化,機率分布也產生變化。
特徵函式

特徵函式與機率密度函式有一對一的關係。因此知道一個分布的特徵函式就等同於知道一個分布的機率密度函式。
套用

X的方差為
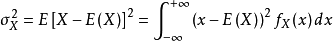
更廣泛的說,設g為一個有界連續函式,那么隨機變數g(X)的數學期望為:





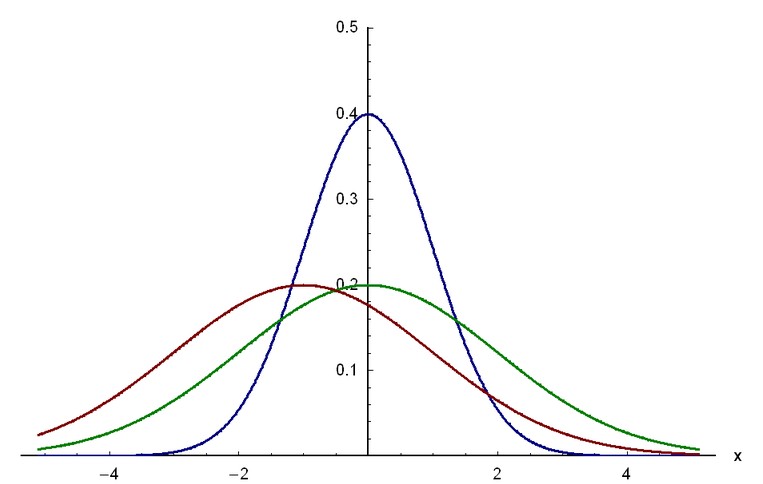 常態分配的機率密度函式
常態分配的機率密度函式

 連續型均勻分布的機率密度函式
連續型均勻分布的機率密度函式
