基本介紹
- 中文名:可積函式
- 外文名:Integrable function
- 定義:如果f(x)在[a,b]上的定積分存在
- 分類:黎曼積分、勒貝格積分
- 充分條件:f(x)在區間[a,b]上連續
- 勒貝格可積性:可積函式是存在積分的函式
定義
黎曼可積
勒貝格積分
黎曼積分與勒貝格積分
黎曼可積的各種條件
充分條件
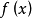
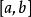
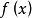
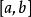
必要條件

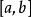
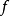
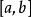
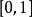
充要條件
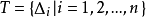


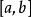
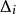
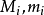


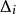

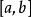
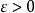
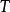

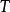

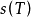
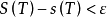

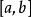
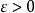
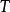
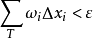
性質
函式乘積的可積性
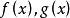

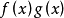
函式絕對值的可積性


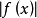

積分值為正的條件


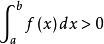


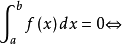


複合函式的可積性






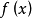
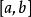
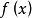
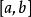

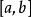
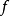
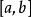
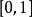
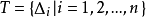


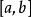
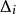
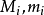


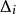

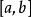
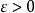
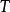

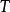

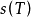
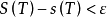

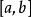
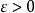
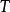
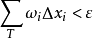
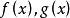

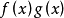


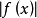



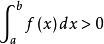


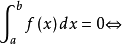







數學上,可積函式是存在積分的函式。除非特別指明,一般積分是指勒貝格積分;否則,稱函式為"黎曼可積"(也即黎曼積分存在),或者"Henstock-Kurzweil可積",等等。黎曼...
勒貝格可積函式是指其勒貝格積分為有限數的函式,簡稱(L)可積函式。在(L)測度有限的集上,有界可測函式都是(L)可積函式。...
絕對亨斯托克可積函式是一類特殊的(H)可積函式。設f(x)是定義在[a,b]上的實值函式,若f(x)與|f(x)|在[a,b]上均(H)可積,則稱f(x)在[a,b]上...
數學上,可積函式是存在積分的函式。除非特別指明,一般積分是指勒貝格積分。否則,稱函式為"黎曼可積"(也即黎曼積分存在),或者"Henstock-Kurzweil可積",等等。...
現規定兩函式f(x)與g(x)與區間[a,b],且兩函式在該區間上可積且平方可積。則積分 記作函式的內積。函式的內積常記作<f(x),g(x)>。...
卷積是分析數學中一種重要的運算。設f(x), g(x)是R1上的兩個可積函式,作積分:可以證明,關於幾乎所有的x∈(-∞,∞) ,上述積分是存在的。這樣,隨著x的不...
它的子區間長度最大值足夠小,函式f的黎曼和都會趨向於一個確定的值,那么f在閉區間[a,b]上的黎曼積分存在,並且定義為黎曼和的極限,這時候稱函式f為黎曼可積的...
可積性條件(integrability condition)亦稱牛朗特一尼倫伯格定理.判斷殆複流形是複流形的準則.複流形自然是一個殆複流形,反之不然.可積性條件是判斷殆複流形上...
可積性所屬現代詞,指的是天文學專有名詞。...... “可積性”是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英...
函式論,含義是實變函式論和復變函式論的總稱,實函式論是研究函式的連續性、可微性和可積性的理論;復變函式論是研究復變數的解析函式性質的理論。以實數作為...
斜坡函式,它是赫維賽德函式的積分形式,記作G(t),脈衝函式也叫狄拉克(Dirac)函式,是赫維賽德函式的廣義導數,記作δ(t)。以上三種都是廣義函式,廣義函式可分為...
多項式基底是將多項式方程式分解為線性函式。基函式傅立葉基底 正弦和餘弦形成平方可積函式的(正交)Schauder 基。 作為一個特例,該集合為:...
函式的積分表示了函式在某個區域上的整體性質,改變函式某點的取值不會改變它的積分值。對於黎曼可積的函式,改變有限個點的取值,其積分不變。對於勒貝格可積的函式...
在數學中,Lp空間是由p次可積函式組成的空間;對應的ℓp空間是由p次可和序列組成的空間。它們有時叫做勒貝格空間,以昂利·勒貝格命名,儘管依據Bourbaki (1987)...
其中∫叫做積分號,f(x)叫做被積函式,x叫做積分變數,f(x)dx叫做被積式,C叫做積分常數或積分常量,求已知函式的不定積分的過程叫做對這個函式進行不定積分。 [1...
積分,長度與面積》建立了測度論和積分論,使一些原先在黎曼意義下不可積的函式按勒貝格的意義變得可積了,可以重建微積分基本定理,從而形成一門新的學科:實變函式論...
與積分相似:連續(或非連續可積)函式的連續和為積分,連續相乘即為積乘。積分表示從一個維度到高一級的維度的轉換,而積乘表示維度的連續變換。...
