勒貝格可積函式是指其勒貝格積分為有限數的函式,簡稱(L)可積函式。在(L)測度有限的集上,有界可測函式都是(L)可積函式。
基本介紹
- 中文名:勒貝格可積函式
- 外文名:integrable function in Lebesgue sense
- 適用範圍:數理科學
簡介
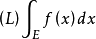
性質


勒貝格可積函式是指其勒貝格積分為有限數的函式,簡稱(L)可積函式。在(L)測度有限的集上,有界可測函式都是(L)可積函式。
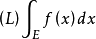


勒貝格可積函式是指其勒貝格積分為有限數的函式,簡稱(L)可積函式。在(L)測度有限的集上,有界可測函式都是(L)可積函式。...
數學上,可積函式是存在積分的函式。除非特別指明,一般積分是指勒貝格積分;否則,稱函式為"黎曼可積"(也即黎曼積分存在),或者"Henstock-Kurzweil可積",等等。黎曼...
勒貝格積分,是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看作是求其函式圖像與軸之間的面積。...
在數學分析中,勒貝格定理,或稱黎曼-勒貝格定理是一個傅立葉分析方面的結果。這個定理有兩種形式,分別是關於周期函式(傅立葉理論中關於傅立葉級數的方面)和關於在...
數學上,可積函式是存在積分的函式。除非特別指明,一般積分是指勒貝格積分。否則,稱函式為"黎曼可積"(也即黎曼積分存在),或者"Henstock-Kurzweil可積",等等。...
[a,b]上的實函式f是黎曼可積的,若且唯若它是有界和幾乎處處連續的。如果[a,b]上的實函式是黎曼可積的,則它是勒貝格可積的。...
勒貝格在《積分與原函式的研究》(Lecons sur l'integration et larecherche des fonctions primitives,1904)中證明了有界函式黎曼可積的充要條件是不連續點構成一...
勒貝格-斯蒂爾傑斯積分(英語:Lebesgue integral)是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看...
可測函式是可測空間之間的保持(可測集合)結構的函式,也是勒貝格積分或實分析中主要討論的函式。數學分析中的不可測函式一般視為病態的。...
黎曼-勒貝格引理(Riemann-Lebesgue lemma)是描述L1中函式傅立葉變換在無窮遠處性質的引理。...
4、函式是可測函式5、在單位區間[0,1]上勒貝格可積,且勒貝格積分值為0(且...狄里克雷函式是周期函式,但是卻沒有最小正周期,它的周期是任意負有理數和正...
函式的積分表示了函式在某個區域上的整體性質,改變函式某點的取值不會改變它的積分值。對於黎曼可積的函式,改變有限個點的取值,其積分不變。對於勒貝格可積的函式...
1)[a,b]上的實函式是黎曼可積的,若且唯若它是有界和幾乎處處連續的。2)如果[a,b]上的實函式是黎曼可積的,則它是勒貝格可積的。...
如果一個函式的積分存在,並且有限,就說這個函式是可積的。一般來說,被積函式不...最常見的積分定義是黎曼積分和勒貝格積分。 黎曼積分 黎曼積分得名於德國數學家...
狹義當儒瓦可積函式是勒貝格可積函式的推廣。當儒瓦(Denjoy,A.)於1912年給出了狹義當儒瓦積分的定義,它同時成為勒貝格積分和黎曼積分的一種推廣。設f(x)是定義在...
絕對積分是使函式與其絕對值同時可積的那種積分,否則稱為非絕對積分。...... 絕對積分是使函式與其絕對值同時可積的那種...勒貝格積分是絕對積分。勒貝格積分是現代...
