基本介紹
定義
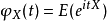




性質
勒維連續定理
反演定理

博赫納-辛欽定理/公理化定義

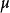




計算性質








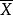

特徵函式的套用
矩




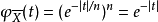
一個例子

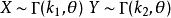

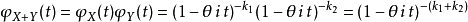



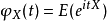






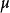












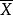





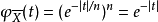

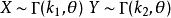

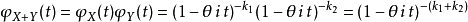


在機率論中,任何隨機變數的特徵函式(縮寫:ch.f,複數形式:ch.f's)完全定義了它的機率分布。...
項目特徵函式(item characteristic function)是一種項目反應理論術語。是指某項目測量的潛在特質和被試對該項目正答機率(θ)之間關係的數學表達式,即項目分數對於所測...
特徵是一個客體或一組客體特性的抽象結果。特徵是用來描述概念的。任一客體或一組客體都具有眾多特性,人們根據客體所共有的特性抽象出某一概念,該概念便成為了特徵...
特徵函式逆轉公式(inversion formula of char-acteristic function)用特徵函式表示分布的重要公式.它解決了特徵函式與分布函式互相惟一確定的問題.特殊函式的逆轉公式為...
特徵函式連續性定理(continuous theorem ofcharacteristic functions)機率論的重要定理之一它使特徵函式成為研究一些極限定理的重要工具...
矩陣的特徵向量是矩陣理論上的重要概念之一,它有著廣泛的套用。數學上,線性變換的特徵向量(本徵向量)是一個非簡併的向量,其方向在該變換下不變。該向量在此...
在集合論中,指示函式是定義在某集合X上的函式,表示其中有哪些元素屬於某一子集A。...... 機率論有另一意思迥異的特徵函式。集X的子集 的指示函式是函式 ,定義...
特徵泛函(characteristic functional)研究隨機過程分布律的重要分析工具。在經典機率論中,富氏分析方法,或者說得更具體一點,特徵函式方法是非常重要的。在研究抽象空間...
在數學中,連續型隨機變數的機率密度函式(在不至於混淆時可以簡稱為密度函式)是一個描述這個隨機變數的輸出值,在某個確定的取值點附近的可能性的函式。而隨機變數的...
特徵軌跡((eigenlocus)用特徵函式在複平面上刻畫系統頻域特性的曲線.它是mXm矩陣G(s)的特徵函式;g ( s)順時針繞閉域月疊}}}EC,Re.I) 0}的周界屍一周...
在數學分析和實變函式中,常常見到一些病態函式,如取整函式y= [x]、純小數函式y= (x)、符號函式y = sgn x、Dirichlet函式、Riemann函式、Heaviside函式θ(t)、...
示性函式有多種含義,它可以指事件的示性函式,即事件發生與否與0,1兩值函式的對應關係。也可以指隨機過程的示性函式,即隨機過程的均值函式、方差函式、相關函式等...
熱力學函式研究這一系統處於平衡態時的熱力學性質,通常需要知道該系統的特徵函式。...... 後,要研究這一系統處於平衡態時的熱力學性質,通常需要知道該系統的特徵函...
正定函式是一個在許多領域都會遇到並且很有用的概念。如機率論中隨機變數的特徵函式就是正定函式。特徵函式比隨機變數的分布函式更易於處理。正定函式概念的提出晚於...
函式形式單調類定理(monotone class theorenfunction form)是測度論與機率論的理論研究中臼一個重要工具。...
在機率論里,機率母函式是指該隨機變數的機率質量函式的冪級數表達式。它也是研究隨機變數分布律的一個重要的分析工具。...
可以使用辛流形(symplectic manifold)的任何平滑的實值函式H來定義哈密爾頓函式。 函式H被稱為哈密爾頓運算元或哈密爾頓能量函式。 然後將辛流形稱為相位空間。 哈密爾頓...
在譜方法中,總是取適當的Sturm-Liouville問題的特徵函式的有限展開來逼近微分方程的解。參考資料 1. 向新民.譜方法的數值分析.北京:科學出版社,2000:68-70 ...
17.3 特徵函式運算元方法 17.4 值的計算方法 17.5 任意變數的一般類 17.6 分布之間的變換 17.7 局部自相關 17.8 瞬時值 17.9 任意變數對的局部值 17.10...
