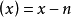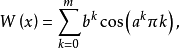在數學分析和實變函式中，常常見到一些病態函式，如取整函式y= [x]、純小數函式y= (x)、符號函式y = sgn x、Dirichlet函式、Riemann函式、Heaviside函式θ(t)、Weierstrass函式W(x) 等等，把它們稱為病態函式(pathological function)，是因為它們的定義及性質都比較特殊，不同於一般的初等函式，但重要的是還和人們的認識水平有關，因為對一些奇特性質難以解釋或找不到直觀背景等原因而稱之為病態，而稱其為病態也只是相對的，隨著科學技術的發展，以及人們所處理問題的日益複雜，一些原來看似病態的函式，現在看來卻是性質良好的，並且還發揮著重要的作用。這些函式是隨著人們對函式概念的本質的深化認識而人為地構造出來的，利用這些函式常常可非從正面或反面說明實分析中某些重要概念和原理，使實分析的理論臻於完善。一般所謂的病態函式，往往指處處連續但處處不可導的函式，如魏爾斯特拉斯函式(Weierstrass函式)，它是由一個無窮級數定義的，可以直觀地想像它，就是一條連續的鋸齒狀折線，但鋸齒的大小無限地小。
基本介紹
- 中文名：病態函式
- 外文名：pathological function
- 提出者：魏爾斯特拉斯
- 所屬學科：數學（數學分析和實變函式）
- 舉例：Weierstrass 函式等
發展歷史,定義,主要函式,
發展歷史
牛頓和萊布尼茲發明微積分後的200年間，直到19世紀末還是安全的，19世紀的數學界的流行觀念是“連續函式必定可微”，相應的函式一般都應該有導數，可微性是指可以逐點計算曲線的斜率，它是微積分的核心特徵。自從微積分發明之日起，就有人認為，由於該學科與運動和量的增長緊密聯繫，因此一個函式的連續性就足以保證導數的存在了。極限是微積分的基本概念，但在微積分嚴密化的進化過程，極限概念一直都缺少精確的表達形式，因為它是建立在幾何直覺基礎之上的。對微積分嚴密化作出最偉大貢獻的法國數學家柯西把極限定義成了清楚而確定的算術概念而非幾何概念，柯西的極限定義運用了數、變數以及函式的概念，而不是運用幾何與動力學直覺，之後柯西又定義了令數學家糾結了近兩千年的無窮小概念。
確立了極限、無窮小和無窮大的概念之後，柯西就能夠定義微積分的核心概念導數了。柯西使導數成為微分的核心概念，然後微分就可根據導數來定義。這樣，柯西給予了導數和微分概念一種形式上的精確性，使微積分的基本概念得到了嚴密的闡述。由於這個原因，柯西被看做是近代意義上的嚴格微積分的奠基者。通過極限概念精確的定義，柯西建立了連續性和無窮級數的理論以及導數、微分和積分的理論。但是柯西的描述里還是有某些細微的邏輯缺陷，一個是無窮集合的概念，一個是數的概念，這由後來的康托爾的努力才進一步完善。此外，在柯西的概念中，變數趨近於一個極限的概念喚起了運動和量的生成的模糊直覺。所以，儘管柯西賦予微積分目前的一般形式，以極限概念為基礎，但是微積分嚴密性的真正權威論述還沒有給出。19世紀數學家“現代分析之父”魏爾斯特拉斯(Karl Weierstrass)登場了。
魏爾斯特拉斯認為柯西的一個變數趨近於一個極限的說法，隱含著連續運動的直覺，魏爾斯特拉斯非常清楚直覺是不可信的，他嘗試以嚴密和精確的形式作為分析學基礎，並且完全獨立於所有幾何直覺。1872年，魏爾斯特拉斯向柏林科學院報告了數學分析史上著名的一個反例——一個處處連續，但處處不可微的三角函式級數，即著名的魏爾斯特拉斯函式，魏爾斯特拉斯函式是一種無法用筆畫出任何一部分的函式，因為每一點的導數都不存在，畫的人無法知道每一點該朝哪個方向畫。魏爾斯特拉斯函式的每一點的斜率也是不存在的。魏爾斯特拉斯用這個“反常”函式來說明用直覺為指導、通過運動來定義的連續曲線，不一定就會有切線。為了保證邏輯的正確性，魏爾斯特拉斯希望把微積分只建立在數的觀念上，由此將它完全與幾何分開。將魏爾斯特拉斯函式在任一點放大，所得到的局部圖形和整體圖形相似。因此，無論如何放大，函式圖像都不會顯得更加光滑，也不存在單調的區間。魏爾斯特拉斯與柯西將導數和積分的定義結合在一起，為微積分的基本概念提供了一種精確性，這種精確性構成了對微積分的嚴密闡述。但就是這個“去幾何化”的反例和特例，在近一個世紀後，開啟了一個全新的幾何時代。魏爾斯特拉斯函式可以被視為第一個分形函式，儘管這個名詞當時還不存在。
定義
病態函式是指在某一方面表現出奇特性質的函式，因為它們具有其他函式不具備的性質，故經常用來作為反例。無論是在微積分理論本身的發展過程中，還是在微積分的教學中，病態函式都起著重要的作用，下面介紹微積分中4 個著名的病態函式：Dirichlet 函式、Cauchy 函式、Riemann 函式和Weierstrass 函式。這些函式在微積分的發展歷史中曾起過重要的作用，直到今天，其中一些函式無論在理論還是在實際中仍然有重要的套用。
主要函式
Dirichlet 函式
函式是微積分研究的基本對象，它的定義看似平淡無奇，但事實上,從其起源到成熟，經歷了一個漫長的過程。在17世紀的Newton和Leibniz時代，微積分研究的主要是幾何曲線(應該和Euclid所產生的深遠影響有關)，而且Leibniz首先使用函式這個名詞描述曲線的一個相關量，到了18世紀，Euler使人們把注意力從曲線轉移到函式，Euler首先區分了常量與變數，並給出了函式的定義：變數的函式是由變數與常量以任何方式構成的解析表達式，這些思想對於曲線來說是一種巨大的進步，但其定義需要通過解析表達式，即公式表示函式。這一定義使得我們現代所接觸到的一些函式不能被稱為函式，再後來，Euler對函式的定義作了改進，如果某些量以如下方式依賴另一些量：當後者變化時，前者也發生變化，則稱前一些量是後一些量的函式。
19 世紀初，Fourier在研究弦振動和熱擴散問題時把函式的Euler定義進行了擴展，指出函式可以在定義域任意取值，但若要理解一個真正“任意”函式的概念，那么必須有人給出一個這樣的函式，Dirichlet 函式就出現在此背景下，因此可以說，該函式的出現,是函式概念正式形成的標誌，它的定義如下，
Dirichlet 函式有一些重要的性質，例如不能畫出該函式的圖像；它是周期函式，卻沒有最小正周期；它在實數集上處處有定義，但處處不連續；可以用它來構造本身非Riemann 可積但其絕對值函式卻可積的例子。這些奇特性質以及由其構造的一些反例對積分理論的發展曾起著重要的促進作用。
Cauchy 函式
在微積分的發展初期，即18 世紀，還沒有嚴格的極限理論，雖然當時許多傑出的數學家如Euler等用微積分這一全新的工具解決了許多在過去被認為是高不可攀的難題，但同樣也發現了一些解釋不清的矛盾(這稱為第二次數學危機 )。許多數學家試圖解決上述矛盾並建立微積分嚴格的基礎，其中Lagrange 曾提出一種方案，用函式的無窮級數(冪級數) 來定義導數(這與現代的觀點恰好相反)，從而把無窮級數作為微積分的基礎。但是，Lagrange的這一想法最終被證明是不可行的，因為Cauchy在1822年給出了一個反例，即如下定義的函式，
Riemann 函式
前文已指出,Cauchy提出了極限的嚴格定義，這是他對微積分的重要貢獻之一。不但如此，他還以此為出發點，用極限給出了微積分中的其他重要概念如連續函式、導數以及積分的定義，這在微積分的發展過程中是具有劃時代意義的。特別是積分的定義，在Cauchy之前，積分一直被認為是微分的逆運算而在微積分的概念中處於次要位置。Cauchy是第一個把積分作為一個獨立的概念並用分割區間的方法來定義的人。他的定義使得在兩個關鍵問題上再無懸念：積分是一種極限,積分的存在同微分無關，然而，應該指出，Cauchy 關於積分的定義遠非完美，因為他的定義僅適用於連續函式或至多有有限多個不連續點的函式。對這一定義進行推廣的是Riemann。他僅假定函式在某一閉區間上是有界的，對這樣的函式提出了他的積分定義，並給出了一個函式在該定義下可積的充分必要條件。因為事先關於函式的連續性沒有做任何假設，因此暗示著某些奇特的函式，比如非常不連續的函式也許是可積的(在他的定義下)。Riemann確實給出了這樣一個函式，其定義如下，
可以證明，函式
在任意有限的區間內具有無限多不連續點，因而可以說是“高度不連續”的然而，同樣可以證明，該函式在閉區間[0，1] 上是Riemann 可積的。這就說明，Riemann關於積分的定義，確實比Cauchy的定義適用性更廣，是它的推廣.另外，這個病態函式的出現還引發了另一個問題，即一個函式為了Riemann可積，可以不連續到何種程度?對這一問題的探討持續了一個多世紀，到了20世紀初，才由Lebesgue給出了完美而且簡潔的答案：一個在閉區間
上有界的函式
在 上Riemann可積的充分必要條件是 在 上幾乎處處連續。
Weierstrass 函式
我們知道，一個可微的函式必定是連續的，人們曾經認為連續函式必定存在可導點，而且除了某些孤立的點外，其餘都是可微的，例如大名鼎鼎的Ampere還曾經“證明”過這樣的結論。事實上，在19 世紀前半期，微積分的教科書都支持這種見解"。然而，Weierstas函式的出現完全扭轉了這一局勢該函式發表於1860年前後，其定義如下，
當然，處處連續但處處不可導的函式遠不止Weiersrass函式一個(但它卻是第一個，也是最著名的一個)。1930年，Van der Waerden給出了另一個(較為簡單)例子。另外，1918年，Wiener給出了Brown運動的數學理論，結果表明Brown運動的樣本軌道就是處處連續但處處不可微的函式。也許有人會問，這些性質奇特的函式除了給出一個反例外，是否還有別的套用? 答案是肯定的。因為20世紀末的數學家們發現，Brown運動可以用來刻畫期權的價格波動(這一發現於1997年獲得了諾貝爾經濟學獎)。粗略地說，期權的價格是隨時間變化的函式，就是處處連續又處處不可微的。
