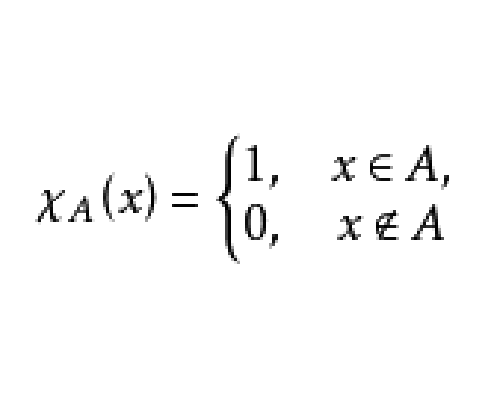示性函式

示性函式有多種含義，它可以指事件的示性函式，即事件發生與否與0,1兩值函式的對應關係。也可以指隨機過程的示性函式，即隨機過程的均值函式、方差函式、相關函式等。還可以指集合的示性函式，即集合的特徵函式。其中事件的示性函式也可以歸於集合的示性函式，二者都是與0,1二值函式相關的。

基本介紹

• 中文名：示性函式
• 外文名：characteristic function
• 所屬學科：數學
• 相關概念：0-1分布，集合，隨機過程等

事件示性函式

依事件出現與否應取1和0的函式。設A是—事件，則

稱做“事件A的示性函式”。事件示性函式是一隨機變數，服從0-1分布。必然事件的示性函式恆為1，下可能事件的示性函式恆為0。

事件的關係和運算與示性函式的關係和運算一一對應。如

若，則；若，則。此外，

藉助示性函式，可以將事件的研究納入隨機變數的研究。

集合的示性函式

集合的特徵函式(characteristic function of a set)亦稱集合的示性函式，與集合一一對應並反映其組成、運算和可測性等特性的簡單函式。可看做集合的函式表示法，該集合的元素由相應特徵函式取值1的點所確定。設X是全集，對任意集合，把函式

稱為集合A的特徵函式或示性函式。特徵函式與相應集合之間有如下關係：

1.；

2.。

3.。

4.對一列集，有

5. 為(L)可測函式A為(L)可測集。

隨機過程的示性函式

為了描述一個隨機過程，必須知道它的有限維分布函式族。然而在計算較高維數的分布函式時，往往在計算上帶來很大的困難。因此，在實際套用中，通常是利用隨機過程的幾個主要特徵來描述。我們知道，在機率論中為了描述隨機變數，通常是用均值、方差和相關係數等示性數來描述。對於隨機過程，均值、方差及相關係數隻不過是時間的函式而已。因此，我們通常稱之為均值函式、方差函式及相關函式，有時把這些函式叫做隨機過程的示性函式。

均值函式

定義1設為隨機過程，如果積分

存在，則稱為該隨機過程的均值函式，有時簡記為。其中和分別為該隨機過程的一維分布函式和一維密度函式。

方差與標準偏差函式

定義2 設為隨機過程，如果積分

存在，稱為該隨機過程的方差函式，有時簡記為。特別地，稱

為隨機過程的標準偏差函式。

相關函式

定義3設為隨機過程，如果積分

存在，則稱為該隨機過程的原點自相關函式。特別地，稱為二階原點矩函式。完全類似，稱

為隨機過程和的原點互相關函式。

稱積分

為隨機過稱的中心自相關函式，完全類似，稱

為隨機過程和的中心互相關函式。

由(2)式及(3)式，可知

比較(1)式和(3)式，還有