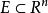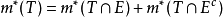可測集

設E ⊂R^n，若對任意的點集T⊂R^n ，有 m*(T)=m*(T∩E)+m*(T∩E^c)，則稱E為Lebesgue可測集，簡稱可測集，可測集的全體記為M，對於可測集E，稱其外測度為測度，記為m(E)。可測集具有許多重要的性質：可測集的補集也是可測集；若A,B為可測集，則A∪B，A∩B，A\B皆為可測集；可測集列的並集和交集分別為可測集。常見的可測集有R^n中的矩體、開集、閉集、Borel集等。

基本介紹

• 中文名：可測集
• 外文名：Measurable set
• 記號1：記可測集的全體為M
• 記號2：記測度為m(E)
• 性質：可測集補集也是可測集
• 套用學科：實變函式

定義

設 ，若對任意的點集 ，有 ，則稱E為Lebesgue可測集，簡稱可測集。

注意事項如下：

（1）可測集的全體記為M，對於可測集E，稱其外測度為測度，記為m(E)。

（2）稱測度為零的可測集為零測集。空集、有限集、可數集皆為零測集。

（3）通常稱定義中的條件為卡氏條件，稱其中的集T為試驗集。

相關定理

零集

零集為可測集。

證明：設E為零集，m*(E)=0，任意A⊂R，因為A∩E⊂E，所以有0≤m*(A∩E)≤m*(E)，得m*(A∩E)=0，於是

故E∈M。

可測集的補集

若E為可測集，則E的補集也是可測集。

可測集的並集交集

若A,B為可測集，則A∪B，A∩B，A\B皆為可測集。

證明：對任意 ，易得 ，依次利用外測度的次可加性、B的可測性（取 為試驗集）以及A的可測性（取T為試驗集），有：

且

故得到。

所以可知A∪B是可測集，從而是可測集，A\B=也是可測集。

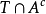
可數可加性

若是互不相交的可測集列，則並集為可測集，且。

證明：對任意的，由外測度的次可加性等性質可知

所以是可測集，令，則有。

可測集列的交與並

（1）若是可測集列，則並集為可測集，且。

（2）若是可測集列，則交集為可測集。

（3）若有遞增可測集列，則，此時對可測集的極限有定義。

（4）若有遞減可測集列，且，則，此時對可測集的極限有定義。

（5）任一可測集均可以表示為一列遞增的有界可測集之並。

（6）任一可測集均可以表示為一列兩兩不交的有界可測集之並。

可測集類

第一類

中的矩體是可測集。

證明：設矩體，對任意矩體，不妨設。記矩體，把分割成有限個互不相交的矩體之並：，則有，從而得到

此時易得，矩體S為可測集。

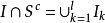
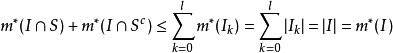
第二類

由中開集的構造可知，每個開集可寫成可列個互不相交的半開半閉的矩體之並，故開集必為可測的。由此易得到如下結論：

開集、閉集、集、集、Borel集皆為可測集。

可測集的等價刻畫

設，則下列條件等價：

（1）E是可測集；

（2）對任意ε>0，存在開集G⊃E，使m*(G\E)<ε；

（3）對任意ε>0，存在閉集F⊂E，使m*(E\F)<ε；

（4）存在集H⊃E，使得m(H\E)=0；

（5）存在集K⊂E，使得m(E\K)=0。