勒貝格可測集是實變函式論的重要概念之一,指勒貝格意義下可求“長度”、“面積”或“體積”的一類集合。
基本介紹
- 中文名:勒貝格可測集
- 外文名:Lebesgue measurable set
- 適用範圍:數理科學
簡介

點集的可測集


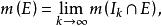
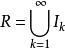
勒貝格可測集是實變函式論的重要概念之一,指勒貝格意義下可求“長度”、“面積”或“體積”的一類集合。



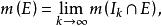
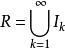
勒貝格可測集是實變函式論的重要概念之一,指勒貝格意義下可求“長度”、“面積”或“體積”的一類集合。...
勒貝格可測集類是集函式的定義域。蘇斯林首先舉出了不是波萊爾集的勒貝格可測集,因而勒貝格可測集類更廣的集類,但並非一切點集都是勒貝格可測的。...
勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛套用於實分析,特別是用於定義勒貝格積分。可以賦予一個體積的集合被稱為勒貝格可測;...
可測函式是可測空間之間的保持(可測集合)結構的函式,也是勒貝格積分或實分析中主要討論的函式。數學分析中的不可測函式一般視為病態的。...
若爾當可測集(Jordan measurable set)是其若爾當內、外容度相等的有界集。有界集A若爾當可測有許多充分必要條件,A的邊界的若爾當容度為0是其一。有界集是...
勒貝格可測函式簡稱(L)可測函式,是比連續函式更廣的一類函式。定義在(L)零測度集上的任何實值函式以及區間上的半連續函式都是(L)可測函式。定義在(L)可測集...
取R的全體子集作為F,設其σ域F',F'包括所有的區間,而且其中的元素都有測度L,且L是區間長度概念的自然推廣,可得到勒貝格測度空間(R,F',L),F'中的元素叫...
可測變換(可測函式)又稱為可測映射,是從一個測度空間到另一個測度空間之間的一個映射,它將前者中的可測集映射為後者中的可測集。可測變換在測度論是十分重要...
波萊爾可測函式(Borel measurable function)亦稱波萊爾函式,是與波萊爾集相適應的可測函式。設f(x)是定義在波萊爾集B⊂Rn上的擴充實值函式,若對任意實數α,點集...
1.4可測集 練習題1 第2章可測函式與依測度收斂 2.1基本概念及主要定理 2.2可測函式 2.3依測度收斂 2.4典型題選解 練習題2 第3章Lebesgue積分...
可以表示為可數個可測集的並集,而且這些可測集的測度均有限,就稱 具有 -有限測度。作為例子,實數集賦以標準勒貝格測度是 -有限的,但不是有限的。為說明之,只要...
維塔利集合是一個勒貝格不可測的集合的例子,以朱塞佩·維塔利命名。維塔利定理就是關於這種集合存在與否的存在性定理,它是一個非構造性的結果。維塔利集合有無窮多...
第一,一個基本空間(即n維歐幾里得空間R)以及這個空間的某些子集構成的集類即L(勒貝格)可測集或某L-S(勒貝格-斯蒂爾傑斯)可測集全體,這個集類對集的代數運算和...
S測度是超實數集*R中的一種測度,是魯賓孫(Robinson,A.)於20世紀60年代初...易證,若B⊂R,則*B是S可測的若且唯若B是勒貝格可測的,而且其值相等。 ...
使機率測度與勒貝格測度相關聯的變數是機率密度函式,具體原理為拉東-尼古丁定理。博雷爾測度與對定義在其上的集合的勒貝格測度結果一致, 然而還有比博雷爾可測集更多的...
性質1,2,3,4全都滿足的測度是不存在的,特別地,直線上必存在不是勒貝格可測的集,這首先是由維塔利(Vitali,G.)於1905年指出的。...
延拓的構造/唯一性與π-λ定理/單調類/單位區間上的勒貝格測度/完備性/不可測集/兩個不可能性定理4.可數機率一般公式/極限集/獨立事件/子域/Borel-Cantelli引理...
二元組( X, F),其中F只要滿足三個條件就可以了, 這樣就可以對 F中的元素定義測度, 所以F中的元素叫可測集,但是這時許多人會犯一個致命的錯誤, 認為對 F...
完備測度(complete measure)亦稱完全測度,是使得零集的任何子集都可測的那種測度。設(Ω,F,μ)是測度空間,如果(Ω,F,μ)中μ零集的子集都是可測集,則稱μ...
則稱ρ是定義在X上的一個測度,Γ中的集合是可測集,不在Γ中的集合是不可...一維勒貝格測度是定義在 的一個含所有區間的σ代數上的、完備的、平移不變的、...
勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛套用於實分析,特別是用於定義勒貝格積分。可以賦予一個體積的集合被稱為勒貝格可測;...
例如,當F是R中的波萊爾集類B時,(R,B)稱為波萊爾可測空間。當F是R中的勒貝格可測集類L時,(R,L)稱為勒貝格可測空間。可測空間是測度的定義域,在一個可...
1.2 頻率測度與勒貝格測度1.3 數列與離散系統1.4 模工均勻分布數列第2章 ...4.1 頻率可測集合族4.1.1 偽隨機事件及性質4.1.2 有限曠代數和有限Borel集4.2...
如果A是勒貝格可測的,δ > 0,則A關於δ的擴張(定義為)也是勒貝格可測的,其測度為。 更廣泛地說,設T是一個線性變換,A是一個R的勒貝格可測子集,則T(A)...
