基本介紹
- 中文名:完備測度
- 外文名:complete measure
- 別名:完全測度
- 概述:μ零集的子集都是可測集
- 舉例:勒貝格測度空間
- 領域:機率論
定義

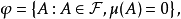
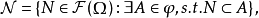
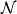
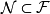


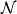
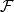
舉例
性質
完備化擴張

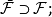
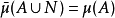
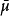
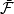
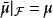
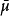
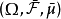
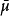
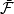
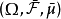
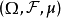

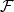
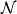

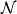
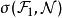

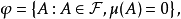
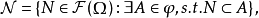
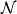
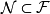


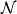
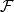

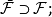
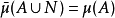
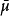
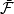
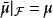
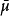
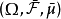
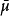
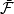
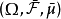
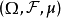

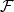
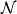

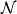
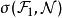
完備測度(complete measure)亦稱完全測度,是使得零集的任何子集都可測的那種測度。設(Ω,F,μ)是測度空間,如果(Ω,F,μ)中μ零集的子集都是可測集,則稱μ...
測度完備化(completion of a measure)亦稱測度完全化,是由任一測度延拓成的完備測度。...
數學上,測度(Measure)是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等。傳統的積分是在區間上進行的,後來人們希望把積分...
完備性是指在數學及其相關領域中,當一個對象具有完備性,即它不需要添加任何其他元素,這個對象也可稱為完備的或完全的。完備性也稱完全性,可以從多個不同的角度來...
零測度就是某個集合的測度為0。數學上,測度(Measure)是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等。...
勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛套用於實分析,特別是用於定義勒貝格積分。可以賦予一個體積的集合被稱為勒貝格可測;...
《機率與測度》是2007年世界圖書出版公司出版的圖書,作者是別林斯里。該書主要內容包括機率、測度、積分、隨機變數及數學期望、分布的收斂的問題、導數與條件期望、...
《廣義模糊集值測度引論》是2009年科學出版社出版的圖書,作者是哈明虎,楊蘭珍。...... 廣義模糊集值測度、廣義模糊集值測度的擴張和完備化、廣義模糊集值測度空間上...
完全性,即完備性。在數學及其相關領域中,一個對象具有完備性,即它不需要添加任何其他元素,這個對象也可稱為完備的或完全的。更精確地,可以從多個不同的角度來...
2. 1 測度與測度空間2.1.1 測度空間2.1.2 半域和域上的測度2.1.3 完備測度2.2 機率測度的延拓和生成2. 2. 1 域上測度延拓定理...
