基本介紹
- 中文名:相對不變測度
- 外文名:relative invariant measure
- 領域:數學
- 性質:不變測度的推廣
- 形式:混沌運動
- 實例:勒貝格測度、哈爾測度
概念,測度,不變測度,混沌運動,勒貝格測度,哈爾測度,
概念
相對不變測度(relative invariant measure )是不變測度的推廣。設一切記號與條目“不變測度”中意義相同。而對任意s∈Ω,存在正實數χ(s),使得μ(A)=χ(s)μ(sA),則稱測度μ為相對不變測度。
測度
測度,是數學術語,釋義是構造一個集函式,它能賦予實數集簇М中的每一個集合E一個非負擴充實數m(E)。我們將此集函式稱為E的測度。測度有計數測度、勒貝格測度、哈爾測度、機率測度等。構造一個集函式,它能賦予實數集簇М中的每一個集合E一個非負擴充實數m(E)。我們將此集函式稱為E的測度。
定義1:構造一個集函式,它能賦予實數集簇М中的每一個集合E一個非負擴充實數m(E)。我們將此集函式稱為E的測度。
定義2:設Γ是集合X上一σ代數,ρ :Γ →R∪{ +∽ }是一集合函式,且ρ滿足:
(1)(非負性)對任意的A∈Γ,有ρ(A)≧0;
(2)(規範性)ρ(Φ) = 0;
(3)(完全可加性) 對任意的一列兩兩不交集合A1,A2,……,An,……有ρ(∪n An)=∑n ρ(An)
則稱ρ是定義在X上的一個測度,Γ中的集合是可測集,不在Γ中的集合是不可測集。特別的,若ρ(X) = 1 ,則稱ρ為機率測度。
不變測度
不變測度是測度的一種。對於出現混沌的一維映射:
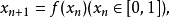
雖然混沌運動軌道的點集{xn}具有對初條件敏感的性質,但是它可以用一個分布函式P(x)來描述。即在區間[0,1]上的每一x處都有一定的機率測度:
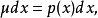
該測度p(x)隨著由xn到xn+1的疊代映射,亦相應地演化。顯然這時存在一個和映射f有關的運算元F(稱Frobenias-Perron運算元),使該測度由μ演化到Fμ,再變到Fμ等。這時方程μ=Fμ的不動點就是不變測度。由於xn是xn+1的逆映射,因此不變測度也意味著:

因為存在不變測度,可知混沌軌道是各態歷經的,此時時間平均就可以用按機率分布的平均來代替。
混沌運動
混沌運動是指在確定性系統中出現不規則的、非周期的、錯綜複雜細節的、不可預見的運動。是一種真正的非線性效應。混沌不是簡單的無序,而更象是不具備周期性和其它明顯對稱特徵的有序態。在理想情況下,混沌狀態具有無窮的內部結構,只要有足夠精密的觀察手段,就可以在混沌態中發現周期和準周期運動。遠離平衡態的系統可能經過突變進入混沌態,它可能與耗散結構交替出現。混沌運動是自然界的一種普遍規律。混沌研究是本世紀70年代中期興起的一場聲勢浩大的科學運動,已出版了許多書名就帶有CHAOS字樣的書,如舒斯特的《確定性混沌》(1984),郝柏林編輯的《混沌》(1986),湯普森和斯特瓦爾特的《非線性動力學與混沌》(1986),霍登編輯的《混沌》(1986),郝柏林編輯的《混沌的方向,》(1987、1988)等等。這些書都是關於非線性動力學中的混沌,基本上代表了今日混沌研究的主流。目前,混沌現象的研究已涉及到數學、物理、力學、天文、氣象、生態和生理等許多領域,甚至套用到社會和經濟等領域。混沌理論還可能有助於更深刻地理解偶然性和必然性等哲學範疇。普列高津的耗散結構理論和H·哈肯的協同理論就是對混沌現象研究所取得的成果。
勒貝格測度
勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛套用於實分析,特別是用於定義勒貝格積分。可以賦予一個體積的集合被稱為勒貝格可測;勒貝格可測集A的體積或者說測度記作λ(A)。一個值為∞的勒貝格測度是可能的,但是即使如此,在假設選擇公理成立時,R的所有子集也不都是勒貝格可測的。不可測集的“奇特”行為導致了巴拿赫-塔斯基悖論這樣的命題,它是選擇公理的一個結果。
如果A是一個區間[a,b], 那么其勒貝格測度是區間長度b−a。開區間(a,b)的長度與閉區間一樣,因為兩集合的差是零測集。 如果A是區間 [a,b] 和 [c,d]的笛卡爾積,則它是一個長方形,測度為它的面積(b−a)(d−c)。康托爾集是一個勒貝格測度為零的不可數集的例子。
哈爾測度
哈爾測度是不恆等於零的不變測度,R上的勒貝格測度在拓撲群上的推廣。設G是局部緊豪斯多夫拓撲群,Ω=G,sx(或xs)是群G內的乘法。此時把G上的非零左不變(右不變)測度稱為G的左不變(右不變)哈爾測度。這種測度是由哈爾(Haar,A.)於1930年引入的。加法群R上哈爾測度即為勒貝格測度。在交換群的情形,左不變哈爾測度與右不變哈爾測度是相同的,在非交換群的情形,二者未必相同。哈爾測度是建立群上的調和分析理論的工具之一。
