基本介紹
- 中文名:不變測度
- 外文名:invariant measure
- 適用範圍:數理科學
簡介
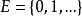


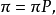
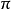
性質
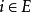
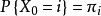
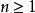
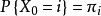

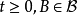
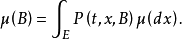

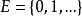


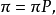
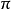
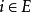
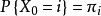
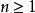
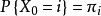

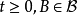
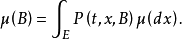
不變測度亦稱平穩分布,是 E 上的一種機率分布,它使馬爾可夫過程成為平穩隨機過程。...... 不變測度亦稱平穩分布,是 E 上的一種機率分布,它使馬爾可夫過程成為平穩...
相對不變測度(relative invariant measure )是不變測度的推廣。測度,是數學術語,釋義是構造一個集函式,它能賦予實數集簇М中的每一個集合E一個非負擴充實數m(E...
擬不變測度是不變測度的推廣。擬不變測度的研究來源於量子物理,它的理論為無限維空間上的微分方程、變分方程的研究提供工具。...
如果𝓕是群Ω上的σ代數,且對於任意的x∈Ω,A∈𝓕有xA={xy|y∈A}∈𝓕,μ是𝓕上的測度,滿足μ(xA)=μ(A),則μ稱為左不變測度。...
《無限維空間上的測度和積分:抽象調和分析(第2版)》包括六章:測度論的某些補充知識,正泛函與運算元環的表示,具擬不變測度的群上調和分析,線性拓撲空間上的擬不變...
如果𝓕是群Ω上的σ代數,且對於任意的x∈Ω,A∈𝓕有Ax={yx|y∈A}∈𝓕,μ是𝓕上的測度,滿足μ(Ax)=μ(A),則μ稱為右不變測度。...
不變測度遍歷分解(ergodic decompositionof invariant measures)反映了不變測度與遍歷不變測度之間的關係.設T為勒貝格空間(X,.},}>上的保測變換,.} (T)表示子...
韋伊測度是群上的一種不變測度,這種測度是由韋伊(Weil,A.)引入的。...... 韋伊測度是群上的一種不變測度,這種測度是由韋伊(Weil,A.)引入的。...
若∀t>0,ξ是μt-上調和的(μt調和的),則稱ξ關於(μt)t>0是超過測度(不變測度)。超過測度性質 編輯 X上的哈爾測度ωX是超過測度。若且唯若∀t>0...
平穩分布是一種機率分布。平穩分布(馬爾可夫鏈的)具有某種不變(或者說平穩)性質的機率分布。...
如果對一切g∈g,g·μ與μ都等價,則稱μ關於群g是擬不變的測度。和連續積分一樣,擬不變測度的研究來源於量子物理。例如,量子場論中交換關係的表示問題實質上...
如果可測變換φ使得μ(φ-1B)=μ(B)對任意B∈B成立,那么φ就稱為保測變換(更詳細一些,φ稱為是保持測度μ不變的變換,μ稱為關於φ不變的測度)。保測...
《隨機環境中的馬爾可夫過程》就其研究的主題而言,含有狀態的分類、狀態空間的分解、遍歷極限與不變測度、大數定律、中心極限定理、不變原理、大偏差原理、Q過程的...
對廣義穩態(特別是混沌穩態),他們利用遍歷理論的Borel不變測度積分定義廣義穩態集合的中心名義值,並據此對廣義穩態進行描述。並給出等效最佳化問題存在條件及其求解算法...
a:線性運算元理論 b:變分法 c:拓撲線性空間 d:希爾伯特空間 e:函式空間 f:巴拿赫空間 g:運算元代數 h:測度與積分 i:廣義函式論 j:非線性泛函分析 k:泛函分析其...
σ是規範化了的∂Bn上的不變測度,σ(Bn)=1。又f(z)在Bn上全純,在 上連續。華羅庚引進並證明了在一般有界圓型星形域上,存在一類柯西積分公式,稱為柯西-...
G fl .f(t,G>並必,則稱f具有域回歸性;具有不變測度的動力系統具有域回歸性;動力系統限制在其中心上具有域回歸性;在一集合的極小吸引中心內有域回歸性等.它...
