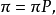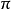韋伊測度

韋伊測度是群上的一種不變測度，這種測度是由韋伊(Weil,A.)引入的。

基本介紹

• 中文名：韋伊測度
• 外文名：Weil measure
• 適用範圍：數理科學

簡介

韋伊測度是群上的一種不變測度，這種測度是由韋伊(Weil,A.)引入的。

設𝓕是局部緊豪斯多夫群G上的σ代數，滿足條件：當A∈𝓕時，對任意的s∈G，有sA∈𝓕。設μ是𝓕上的σ有限測度。如果μ滿足下列條件，則稱μ是G上的左不變韋伊測度：

1、μ(sA)=μ(A)；

2、當f(x)為𝓕可測時，f(xy^-1)必為𝓕×𝓕可測的。

不變測度

不變測度亦稱平穩分布(stationary distribution)。

不變測度是E 上的一種機率分布，它使馬爾可夫過程成為平穩隨機過程。給定以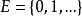為狀態空間的時齊馬爾可夫鏈，其一步轉移陣為 P 。如果存在 E 上的機率分布，滿足矩陣方程

則稱為鏈的平穩分布，或稱為轉移陣 P 的不變測度。

提出者背景

安德烈·韋伊（André Weil，公元1906年5月6日─1998年8月6日）是一位法國數學家，是早逝的思想家西蒙娜·韋伊的兄長，兄妹兩人皆身體力行反對納粹。他是巴黎科學院院士和美國國家科學院外籍院士。

韋伊的主要貢獻在連續群和抽象代數幾何學紀30年代末，他研究了拓撲群上的積分問題，並於1940年完成了專著《拓撲群上的積分及其套用》。這本書反映出的數學結構主義體現了布爾巴基學派的觀點，開闢了群上調和分析的新領域。40年代，他力圖把代數幾何學建立在抽象代數和拓撲學的基礎上，建立了嚴整的代數幾何學體系。