σ域是由樣本空間一些集合為元素(通常包括 )組成的集合。
理論內容,示性函式,隨機變數,
理論內容

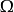
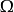

1. 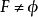
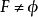
2. 若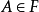 ,有
,有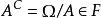
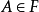
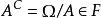
3. 若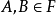 ,有
,有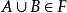
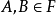
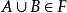
則這個 被稱為
被稱為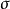 域,也被稱為
域,也被稱為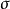 代數。
代數。

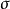
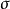
示性函式
定義事件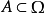 (樣本空間),
(樣本空間),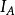 是
是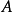 的示性函式:
的示性函式: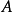 發生,
發生,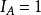 ;
;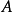 不發生,
不發生,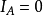 。
。
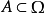
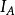
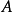
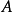
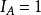
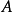
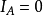
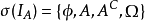
隨機變數
以二值隨機變數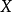 為例,
為例,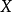 只取0和1
只取0和1
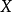
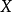
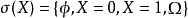
對於多值的隨機變數,表達更複雜,如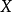 可取0、1和2
可取0、1和2
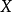
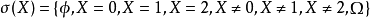
可以看出,由於事件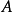 的示性函式
的示性函式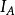 是一個二值隨機變數,二者定義是吻合的,只是表示方法有些差異。
是一個二值隨機變數,二者定義是吻合的,只是表示方法有些差異。
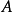
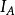
σ域是由樣本空間一些集合為元素(通常包括 )組成的集合。

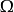
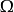

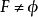
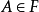
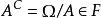
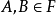
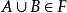

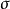
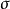
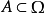
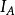
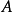
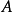
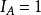
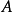
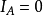
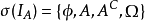
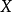
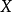
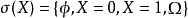
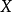
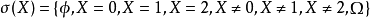
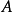
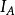
σ域是由樣本空間一些集合為元素(通常包括 )組成的集合。...... σ域是由樣本空間一些集合為元素(通常包括 )組成的集合。目錄 1 理論內容 2 示性函式 3 隨...
在數學中,某個集合X上的σ代數(σ-algebra)又叫σ域 ,是X的所有子集的集合(也就是冪集)的一個子集。這個子集滿足對於可數個集合的並集運算和補集運算的封閉...
設(Ω,𝓕)及(Ω2,𝓕2)是兩個可測空間,由C作為空間Ω1×Ω2上的集類所生成的σ代數σ(C)稱為𝓕1與𝓕2的乘積σ代數。...
(1) 為σ域,(2)令 ,則 是 上測度, ,且當μ為機率測度時 亦然;(3) 是完備測度空間,即 在 上是完備的。注:定理中的 稱為 的完備化擴張。由上定理,...
取R的全體子集作為F,設其σ域F',F'包括所有的區間,而且其中的元素都有測度L,且L是區間長度概念的自然推廣,可得到勒貝格測度空間(R,F',L),F'中的元素叫...
