Sturm-Liouville理論是由 數學家Jacques Charles François Sturm (1803–1855) 和Joseph Liouville (1809–1882)提出的,它是一個二階線性微分方程,在數學,尤其是微分方程求解問題上有重要套用.
基本介紹
- 中文名:Sturm-Liouville理論
- 外文名: Sturm-Liouville theory
- 套用學科:數學
定義










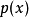
性質

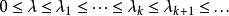


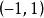
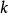

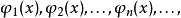

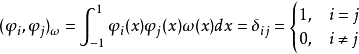
Sturm-Liouville理論是由 數學家Jacques Charles François Sturm (1803–1855) 和Joseph Liouville (1809–1882)提出的,它是一個二階線性微分方程,在數學,尤其是微分方程求解問題上有重要套用.










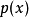

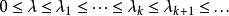


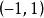
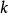

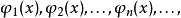

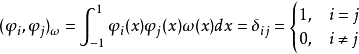
Sturm-Liouville理論是由 數學家Jacques Charles François Sturm (1803–1855) 和Joseph Liouville (1809–1882)提出的,它是一個二階線性微分方程,在數學,尤其是...
主要內容包括:直升機各種飛行狀態的動量理論、渦流理論和葉素理論,並且除對正常...9.1 斯圖姆-柳維葉(Sturm-Liouville)理論9.2 揮舞平面的運動 9.2.1 剛體揮舞...
《線性魯棒控制的理論與計算》是大連理工大學學術著作出版出版的圖書,作者:吳志剛...5.3.1 Hamilton及Sturm-Liouville型微分方程離散化5.3.2 混合能矩陣合併公式...
趙愛民和李美麗等編著的《微分方程基本理論》是在作者多年主講研究生“微分方程...2.4 Sturm-Liouville特徵值問題第3章 穩定性理論基礎3.1 穩定性定義...
《局部重力場逼近理論和方法》是1997年4月1日測繪出版社出版的圖書。...三、球諧函式的Sturm-Liouville型方程四、球冠諧分析5.4 重力歸算及其譜解...
以及對包括振動理論的施圖姆。劉維爾(Sturm-Liouville)型邊值問題的研究。接下來引入動力系統的概念,並對連續系統和離散系統討論穩定性,包括穩定流形和哈特曼。...
3.6Sturm-Liouville理論 3.7自伴運算元的譜定理 3.8習題 第4章Banach空間中的微積分 4.1Frechet導數 4.2向量值函式的積分 4.3Newton法 4.4若干存在性定理...
第四章 Fourier級數和Sturm.Liouville理論§4.1 正交性和Fourier級數定義§4.2 Four-ier級數收斂定理§4.3 正弦級數和餘弦級數及其套用...
虧指數及判定、自伴延拓、譜染特點、譜分解等,有限區間情形給出Liouville、Sturm和泛函分析三種處理.無限區間情形,詳細討論了二階Smrm-Liouville運算元經典的Weyl理論、...
時間尺度上Sturm-Liouville理論、孤立子理論、複分析理論、分數階微分方程建模與套用等領域已經取得了豐富的研究成果,獲得了一批標誌性研究成果,奠定了本方向的學術地位...
通過解積分方程得到微分方程的解,這是斯圖姆-利烏維爾理論最有意義的一點。中文名 斯圖姆與利烏維爾變換 外文名 Sturm-Liouville transformation 分類 計算機 ...
J-自伴微分運算元譜理論的研究及其定量定性分析;非自伴微分運算元的特徵問題;不定的Sturm-Liouville問題的研究;Volterra—Stieltjes積微分運算元理論等,這些成果發表在《數學...
(數學物理方程)的建立、物理思想的形成和數學方法套用於物理過程的理論體系;(2)...§3.4 Sturm-Liouville問題習題三第四章 Green函式法§4.1 6函式...
習題七附錄I Sturm-Liouville理論附錄II Bessel函式附錄III Legendre多項式附錄IV Fourier變換表和Laplace變換表習題答案與提示參考文獻 [1] ...
本書比較全面地介紹了偏微分方程基本解理論,求解波動方程的特徵線法,作為特殊函式理論基礎的Sturm-Liouville理論, 三種類型邊值問題Green函式的求法;特別介紹了用...
介紹數學模型的導出和各類定解問題的解題方法,然後再討論三類典型方程的基本理論...3. 5Sturm-Liouville問題習題34調和方程與格林(Green) 函式法4. 1Laplace方程...
許多重要的邊值問題屬於Sturm-Liouville問題。這類問題的分析會和微分運算元的本徵...許多偏微分方程領域的理論提出是為要證明科學及工程套用的許多邊值問題都是適定...
(7)量子力學中斯圖謨-劉維爾本徵值問題(Sturm-Liouvilleeigenvalue problem)的...“伽羅瓦理論”(Galois Theory)一課,準備以范·德·瓦爾登(B.L.Van der...
《高等學校數學系列教材·積分方程論(修訂版)》介紹積分方程中的Fredholm理論、...3.5.1 Sturm-Liouville問題 3.5.2 二階正則微分運算元的逆 3.5.3 一般情況 ...
