在數學分析中,勒貝格定理,或稱黎曼-勒貝格定理是一個傅立葉分析方面的結果。
這個定理有兩種形式,分別是關於周期函式(傅立葉理論中關於傅立葉級數的方面)和關於在一般實數域R上定義的函式(傅立葉變換的方面)。在任一種形式下,定理都說明了可積函式在傅立葉變換後的結果在無窮遠處趨於0。這個結果也可以適用於局部緊緻的阿貝爾群。
基本介紹
- 中文名:勒貝格定理
- 外文名:Lebesgue lemma
- 學科:數學
歷史
定理的敘述



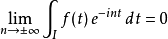




在數學分析中,勒貝格定理,或稱黎曼-勒貝格定理是一個傅立葉分析方面的結果。
這個定理有兩種形式,分別是關於周期函式(傅立葉理論中關於傅立葉級數的方面)和關於在一般實數域R上定義的函式(傅立葉變換的方面)。在任一種形式下,定理都說明了可積函式在傅立葉變換後的結果在無窮遠處趨於0。這個結果也可以適用於局部緊緻的阿貝爾群。



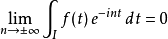



在數學分析中,勒貝格定理,或稱黎曼-勒貝格定理是一個傅立葉分析方面的結果。這個定理有兩種形式,分別是關於周期函式(傅立葉理論中關於傅立葉級數的方面)和關於在...
在數學分析和測度論中,勒貝格控制收斂定理提供了積分運算和極限運算可以交換運算順序的一個充分條件。在分析逐點收斂的函式數列的勒貝格積分時,積分號和逐點收斂的...
黎曼-勒貝格定理(Riemann-Lebesgue's Theory)提出了所有函式的傅立葉展開均收斂於其自身,黎曼-勒貝格定理在信號處理、傅立葉分析上有重要的套用。Riemann-Lebesgue...
數學上,勒貝格微分定理是實分析的一條定理。這條定理大致是說,一個局部可積函式在幾乎每點的值,都是函式在該點為中心的無限小的球上的平均。換言之,該函式的...
波萊爾定理,即海涅-博雷爾定理,在數學分析中,海涅-博雷爾定理(Heine–Borel theorem)或有限覆蓋定理、博雷爾-勒貝格定理(Borel–Lebesgue theorem),以愛德華·海涅 和...
黎曼-勒貝格引理(Riemann-Lebesgue lemma)是描述L1中函式傅立葉變換在無窮遠處性質的引理。...
在數學分析中,海涅-博雷爾定理(Heine–Borel theorem)或有限覆蓋定理、博雷爾-勒貝格定理(Borel–Lebesgue theorem),以愛德華·海涅 和埃米爾·博雷爾命名。定理的主要...
在測度論中,法圖引理說明了一個函式列的下極限的積分(在勒貝格意義上)和其積分的下極限的不等關係。法圖引理的名稱來源於法國數學家皮埃爾·法圖(Pierre Fatou),...
四、有限覆蓋定理(博雷爾-勒貝格定理,海涅-波雷爾定理)閉區間上的任意開覆蓋,必有有限子覆蓋。或者說:閉區間上的任意一個開覆蓋,必可從中取出有限個開區間來...
