基本介紹
歷史
方差的定義







方差的性質

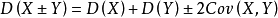






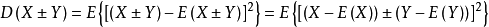











種類及計算
離散型方差



連續型方差
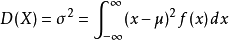




隨機變數的期望和方差
離散型

連續型



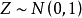
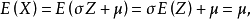

示例
 測量結果
測量結果公式
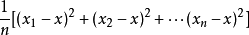
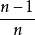



 方差
方差統計學意義










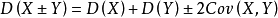






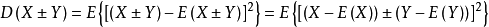














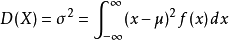








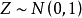
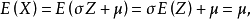

 測量結果
測量結果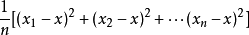
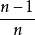



 方差
方差
方差是在機率論和統計方差衡量隨機變數或一組數據時離散程度的度量。機率論中方差用來度量隨機變數和其數學期望(即均值)之間的偏離程度。統計中的方差(樣本方差)是...
方差分析(Analysis of Variance,簡稱ANOVA),又稱“變異數分析”,是R.A.Fisher發明的,用於兩個及兩個以上樣本均數差別的顯著性檢驗。 由於各種因素的影響,研究所...
方差的概念與計算公式,例1 兩人的5次測驗成績如下:X: 50,100,100,60,50 E(X)=72;Y: 73, 70, 75,72,70 E(Y)=72。平均成績相同,但X 不穩定,對...
先求出總體各單位變數值與其算術平均數的離差的平方,然後再對此變數取平均數,就叫做樣本方差。樣本方差用來表示一列數的變異程度。樣本均值又叫樣本均數。即為樣本...
方差公式是一個數學公式,是數學統計學中的重要公式,套用於生活中各種事情,方差越小,代表這組數據越穩定,方差越大,代表這組數據越不穩定。...
相關字母表示: 表型方差:P; 純合體自交系的方差Q;環境方差E;總遺傳方差G; 顯性遺傳方差D;加性遺傳方差A;上位性方差I;狹義遺傳力M;廣義遺傳力H。 公式:E=Q...
根據試驗結果,怎樣找出有顯著作用的因素,以及找出在怎樣的水平和工藝條件下能使指標最優以達到優質和高產的目的,這就是方差分析(Analysis of Variance 簡稱ANOVA)所...
組內方差指方差分析中的隨機誤差的方差。 在方差分析模型中,觀測值方差的各個分量為方差分量,方差分量的概念是針對含隨機效應的方差分析模型引進的,因此稱這樣的...
隨機向量各分量的方差之和。 ...... 隨機向量各分量的方差之和。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,第72頁 V百科往期回...
組間方差是各組平均數對總平均數離差平方的算術平均數。而總方差、組內方差和組間方差三者間的關係如下:總方差=組內方差+組間方差;組間方差的計算方法:先求...
同方差性是經典線性回歸的重要假定之一,指總體回歸函式中的隨機誤差項(干擾項)在解釋變數條件下具有不變的方差。計量經濟學中, 一組隨機變數具備同方差即指線性...
方差分析就是對試驗數據進行分析,檢驗方差相等的多個正態總體均值是否相等,進而判斷各因素對試驗指標的影響是否顯著,根據影響試驗指標條件的個數可以區分為單因素方差...
方差分析表(analysis of variance table)是指為了便於進行數據分析和統計判斷,按照方差分析的過程,將有關步驟的計算數據,例如差異來源、離差平方和、自由度、均方和...
均值—方差模型是由H.M.Markowitz(哈里·馬科維茨)在1952年提出的風險度量模型。馬科維茨把風險定義為期望收益率的波動率,首次將數理統計的方法套用到投資組合選擇...
樣本中各數據與樣本平均數的差的平方和的平均數叫做樣本方差;樣本方差的算術平方根叫做樣本標準差。樣本方差和樣本標準差都是衡量一個樣本波動大小的量,樣本方差或...
協方差(Covariance)在機率論和統計學中用於衡量兩個變數的總體誤差。而方差是協方差的一種特殊情況,即當兩個變數是相同的情況。協方差表示的是兩個變數的總體的...
方差(variance)是在機率論和統計方差衡量隨機變數或一組數據時離散程度的度量。方差反映了樣本數據圍繞樣本平均值變化的情況,方差值越小,表明數據越靠近平均值,離散...
方差法是度量風險投資的常用方法。將風險投資的收益視為一個隨機變數,則它的方差就代表不確定程度或者說風險程度。方差是反映隨機變數與其期望值的偏離程度的數值,是...
總體方差是一組資料中各數值與其算術平均數離差平方和的平均數。 ...... 總體方差是一組資料中各數值與其算術平均數離差平方和的平均數。 中文名 總體方差 外文...
標準差(Standard Deviation) ,中文環境中又常稱均方差,是離均差平方的算術平均數的平方根,用σ表示。標準差是方差的算術平方根。標準差能反映一個數據集的離散...
標準差公式是一種數學公式。標準差也被稱為標準偏差,或者實驗標準差,公式如下所示:標準差=方差的算術平方根=s=sqrt(((x1-x)^2 +(x2-x)^2 +...(...
標準差(Standard Deviation) ,中文環境中又常稱均方差,但不同於均方誤差(mean squared error,均方誤差是各數據偏離真實值的距離平方的平均數,也即誤差平方和的...
