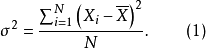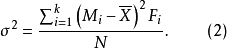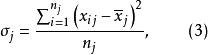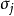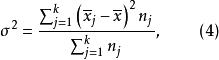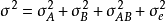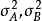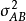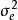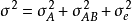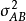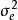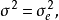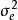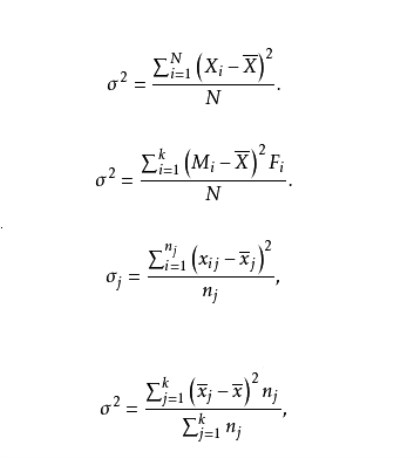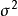組內方差

組內方差指方差分析中的隨機誤差的方差。 在方差分析模型中，觀測值方差的各個分量為方差分量，方差分量的概念是針對含隨機效應的方差分析模型引進的，因此稱這樣的模型為方差分量模型。對於這樣的模型，方差分析的基本假設是通過方差分量來表述的，隨機誤差的方差分量，亦稱做“組內方差”；其餘方差分量則統稱做”組間方差”，或分別稱做“主效應方差分量”和“互動效應方差分量”。

基本介紹

• 中文名：組內方差
• 外文名：intraclass variance
• 所屬學科：數學
• 所屬問題：統計學（方差分析）
• 簡介：方差分析中的隨機誤差的方差
• 別名：主效應方差分量
• 相關概念：方差分析，方差分量等

基本概念

方差(variance)是變數與其算術平均數之差平方的算術平均數，記為。也就是說，標準差的平方即為方差。方差也是最廣泛使用的離散程度測量值。根據研究對象範圍差異方差可分為總方差、組內方差和組間方差。

總方差是由總體變數值和總體算術平均數計算出來的方差。見式(1)和式(2)。反映總體內所有變數值差異程度。

未分組：

分組:

組內方差是由各組變數值和組內算術平均數計算出來的方差。反映組內內變數值差異程度。

式(3)中，是第j組的組內方差，是第j組的單位數。

組間方差是由各組算術平均數和總體算術平均數計算出來的方差。反映各組算術平均值的差異程度。

式中，k為分組數。

相關說明

套用標準差測定總體的標誌變動度（標誌即“變數”），應包括總體各個單位標誌值對平均數的離差。而按組距分配數列計算的標準差，只是反映各組平均數對總平均數的組間離差，沒有反映各組中各單位標誌值對組平均數的組內離差。兩者計算結果是不同的。這就要求我們測定現象總體的標誌變動度時，除研究整個總體的標誌變動度外，還要研究構成總體各組的組間標誌變動度和組內標誌變動度。

總體標誌變動度和組間標誌變動度、組內標誌變動度的關係，在數量上表現為總方差和組間方差、組內方差的關係。總方差是總體各個單位標誌值對總平均數的標準差的平方。組間方差是總體各組平均數對總平均數的標準差的平方。組內方差是組內各單位標誌值對組平均數的標準差的平方。

方差分量

方差分量是方差分析模型中，觀測值的方差σ²的各個分量。例如，對於雙向隨機效應方差分析

有四個方差分量，主因子效應方差分量，互動效應方差分量，隨機誤差方差分量。對於固定效應因子為A，隨機效應因子為B的混合方差分析模型，

有三個方差分量，B的效應的方差分量，互動因子A×B的效應的方差分量，和隨機誤差方差分量。對於單向或雙向方差分析，有

只有隨機誤差方差分量。

方差分量的概念是針對含隨機效應的方差分析模型引進的，因此稱這樣的模型為方差分量模型。對於這樣的模型，方差分析的基本假設是通過方差分量來表述的。隨機誤差方差分量，亦稱做“組內方差”；其餘方差分量則統稱做“組間方差”，或分別稱做“主效應方差分量”和 “互動效應方差分量”。