離散度分析法是測度一組數據分散程度的方法。分散程度反映了一組數據遠離其中心值的程度，因此也稱為離中趨勢。從集中趨勢和分散程度兩個方面才能完整的說明一組數據的變動趨勢。集中趨勢的測度值是對數據水平的一個概括性度量，它對一組數據的代表程度取決於該組數據的離散水平。數據的分散程度越小，集中趨勢的測度值對這組數據的代表性就越好，反之，分散程度越大，代表性就越好。
基本介紹
- 中文名：離散度分析法
- 外文名：Discrete analysis method
- 所屬學科：數學（統計學）
- 別名：離中趨勢
- 相關概念：異眾比例、方差、離散係數等
離散度分析法的定義,離散度分析法的內容,異眾比例,分位差,方差和標準差,離散係數,離散度分析法的比較,
離散度分析法的定義
離散度分析法是測度一組數據分散程度的方法。分散程度反映了一組數據遠離其中心值的程度，因此也稱為離中趨勢。從集中趨勢和分散程度兩個方面才能完整的說明一組數據的變動趨勢。集中趨勢的測度值是對數據水平的一個概括性度量，它對一組數據的代表程度取決於該組數據的離散水平。數據的分散程度越小，集中趨勢的測度值對這組數據的代表性就越好，反之，分散程度越大，代表性就越好。
數據的分散程度是數據分布的另一個重要的特徵。集中趨勢和分散程度是社會經濟現象相互聯繫的兩個重要的特徵。與測度集中趨勢對於不同的數據類型採用不同的測度值一樣，根據不同的數據類型，測度分散程度的測度值也是不同的。主要包括異眾比例、分位差、方差和標準差以及測度相對離散程度的離散係數等。
離散度分析法的內容
異眾比例
異眾比例主要用於測度分類數據的分散程度。它是指非眾數組的頻數占總頻數的比率，用
表示。設一組數據共分為K個不同類別，每個類別的頻數分別為
，則異眾比例的計算公式為：
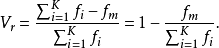
異眾比例的主要作用是衡量眾數對一組數據的代表程度。異眾比例越大，說明非眾數組的頻數占總頻數的比重越大，眾數作為這組數據的代表值的代表性就越差。反之，代表性就越好。雖然，對於順序數據和數值型數據也可以計算異眾比例，但異眾比例主要用於測度分類數據的分散程度。
分位差
分位差主要用於測度順序數據的分散程度。它是指分位數之間的差距。套用最為廣泛的分位差主要是與四分位數對應的四分位差，也稱為四分位間距，它是上四分位數和下四分位數之差，用
表示，其計算公式為：
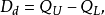
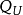
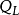
四分位差反映了一組數據處於中間位置的50%數據的離散程度，其數值越小，說明中間的數據越集中，反之，則說明中間的數據比較分散。由於四分位差僅由2個處於四分位點出的數值之差決定，與其他數值沒有關係，因此四分位差不受極值的影響。此外，中位數處於數據的中間位置，因此四分位數的大小在一定程度上反映了中位數對一組數據代表性的好壞。除順序數據外，數值型數據也可計算四分位差，但分類數據不能。
方差和標準差
方差和標準差主要用於測度數值型數據的分散程度。方差是指一組數據各個值與其均值離差平方的平均數，標準差是方差的平方根。方差和標準差的數值越大，說明數據的分散程度越高。反之，則說明數據的分散程度越低。方差和標準差的計算公式對於分組的數值型數據和未分組的數值型數據有所不同。對於未分組數據，設一組數據為
，則方差為:
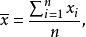
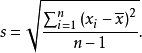
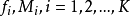
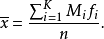
與方差不同的是，標準差與一組數據的各個值的計量單位相同，是具有量綱的，其實際意義比方差清楚。因此，在實際進行分析時，更多的採用標準差作為測度數據分散程度的測度值。
比如，一組數據為25，28，31，34，37，40，43。為計算去方差和標準差，先計算其均值為：
方差和標準差是根據一組數據中的全部數據計算得出的，它反映了這組數據中每個數據與其均值相差的程度，因此他能正確的反映出這組數據的分散程度，在實際中套用得最為廣泛。
離散係數
上面介紹的方差和標準差反映的是數值型數據分散程度的絕對值，它的數值越大，說明數據的分散程度越高。但我們根據其計算公式不難發現方差和標準差測度數據分散水平時存在兩個方面的特徵：一方面方差和標準差數值的大小取決於原本這組數據的值的大小，也就是與這組數據的平均大小水平有關，其平均水平較大，其標準差一般也越大；另一方面方差和標準差的計量單位要么是原來數據計量單位的平方，要么與原計量單位一致，因此採用不同的計量單位，其分散程度的測量值也會不同。因此，對於平均水平不同或計量單位不同的兩個不同的總體，是不能用方差或標準差來比較兩者的分散程度高低的(在下面的例子中將直觀的發現這一點)。這樣，為消除數據值水平高低和計量單位不同對分散程度測量值的影響，需要計算離散係數。離散係數也稱為變異係數，是一組數據的標準差與其均值之比，用來測度相對離散程度。用公式表示為：
離散係數主要用於比較多組數據之間的離散程度。離散係數大的說明數據的分散程度也大，反之，離散係數小的說明數據的分散程度也小。這樣就解決了不同組數據之間由於數據值水平相差懸殊或計量單位不同而不能直接用方差或標準差等絕對指標直接比較它們的分散程度的問題。
例1 A地家電行業銷售額的均值為536.25萬元，標準差為309.19萬元，則離散係數為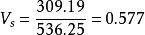
。B地家電行業銷售額的均值為32.51萬元，標準差為23.09萬元，則離散係數為
。
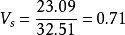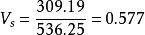
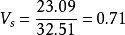
從上例中我們不難發現，若從標準差出發判斷兩地銷售額的分散程度，則A地標準差309.19>B地標準差23.09，但造成A地標準差較大的原因其實是A地銷售額數據值水平遠高於B地，因此當消除數據水平高低的影響後，計算得到的A地的離散係數0.577<B地的離散係數0.71。兩地相比，說明B地的銷售額的分散程度大於A地，其均值32.51的代表性也就較小。
離散度分析法的比較
反映一組數據分散程度的各個測度值適用於不同類型的數據。對於分類數據，主要用異眾比例來測度其離散程度；對於順序數據，雖然也可以用異眾比例，但主要用分位差來測度其分散程度，其中最常用的是四分位差；對於數值型數據，異眾比例和分位差都適用於測度其分散程度，但主要用方差和標準差來測度其分散程度，方差和標準差利用了一批數據中的所有信息，準確性更高。當需要對多組數據的分散程度進行比較時，則使用離散係數。因此，在具體的套用中選用哪一種測度值來衡量數據的分散程度，必須根據我們所掌握的數據類型和分析目的來確定。
