基本介紹
- 中文名:二項分布
- 外文名:Binomial Distribution
- 提出者:伯努利
- 涉及實驗:伯努利試驗;兩點分布
- 屬於:機率論與數理統計
- 套用學科:大氣科學;氣候學;計算機科學
定義,統計學定義,醫學定義,概念,性質,圖形特點,套用條件,套用實例,
定義
統計學定義
在機率論和統計學中,二項分布是n個獨立的是/非試驗中成功的次數的離散機率分布,其中每次試驗的成功機率為p。這樣的單次成功/失敗試驗又稱為伯努利試驗。實際上,當 時,二項分布就是伯努利分布,二項分布是顯著性差異的二項試驗的基礎。
時,二項分布就是伯努利分布,二項分布是顯著性差異的二項試驗的基礎。

醫學定義
在醫學領域中,有一些隨機事件是只具有兩種互斥結果的離散型隨機事件,稱為二項分類變數(dichotomous variable),如對病人治療結果的有效與無效,某種化驗結果的陽性與陰性,接觸某傳染源的感染與未感染等。二項分布(binomial distribution)就是對這類只具有兩種互斥結果的離散型隨機事件的規律性進行描述的一種機率分布。
考慮只有兩種可能結果的隨機試驗,當成功的機率(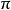 )是恆定的,且各次試驗相互獨立,這種試驗在統計學上稱為伯努利試驗(Bernoulli trial)。如果進行
)是恆定的,且各次試驗相互獨立,這種試驗在統計學上稱為伯努利試驗(Bernoulli trial)。如果進行 次伯努利試驗,取得成功次數為
次伯努利試驗,取得成功次數為 的機率可用下面的二項分布機率公式來描述:
的機率可用下面的二項分布機率公式來描述: 二項分布公式
二項分布公式
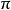


 二項分布公式
二項分布公式P=C(X,n)*π^X*(1-π)^(n-X)
式中的n為獨立的伯努利試驗次數,π為成功的機率,(1-π)為失敗的機率,X為在n次伯努里試驗中出現成功的次數,表示在n次試驗中出現X的各種組合情況,在此稱為二項係數(binomial coefficient)。
所以的含義為:含量為n的樣本中,恰好有X例陽性數的機率。
概念
二項分布(Binomial Distribution),即重複n次的伯努利試驗(Bernoulli Experiment),用ξ表示隨機試驗的結果。如果事件發生的機率是P,則不發生的機率q=1-p,N次獨立重複試驗中發生K次的機率是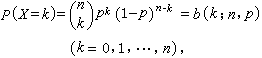 二項分布公式
二項分布公式
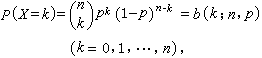 二項分布公式
二項分布公式P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k),其中C(n, k) =n!/(k!(n-k)!),注意:第二個等號後面的括弧里的是上標,表示的是方冪。
那么就說這個屬於二項分布。其中P稱為成功機率。記作ξ~B(n,p)
期望:Eξ=np;
方差:Dξ=npq;
其中q=1-p
證明:由二項式分布的定義知,隨機變數X是n重伯努利實驗中事件A發生的次數,且在每次試驗中A發生的機率為p。因此,可以將二項式分布分解成n個相互獨立且以p為參數的(0-1)分布隨機變數之和.
設隨機變數X(k)(k=1,2,3...n)服從(0-1)分布,則X=X(1)+X(2)+X(3)....X(n).
因X(k)相互獨立,所以期望:

方差:
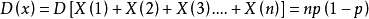
證畢。
如果
1.在每次試驗中只有兩種可能的結果,而且是互相對立的;
2.每次實驗是獨立的,與其它各次試驗結果無關;
3.結果事件發生的機率在整個系列試驗中保持不變,則這一系列試驗稱為伯努利實驗。
在這試驗中,事件發生的次數為一隨機事件,它服從二次分布。二項分布可以用於可靠性試驗。可靠性試驗常常是投入n個相同的式樣進行試驗T小時,而只允許k個式樣失敗,套用二項分布可以得到通過試驗的機率。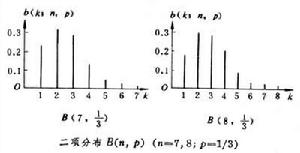 二項分布
二項分布
 二項分布
二項分布若某事件機率為p,現重複試驗n次,該事件發生k次的機率為:P=C(n,k)×p^k×(1-p)^(n-k)。C(n,k)表示組合數,即從n個事物中拿出k個的方法數。
性質
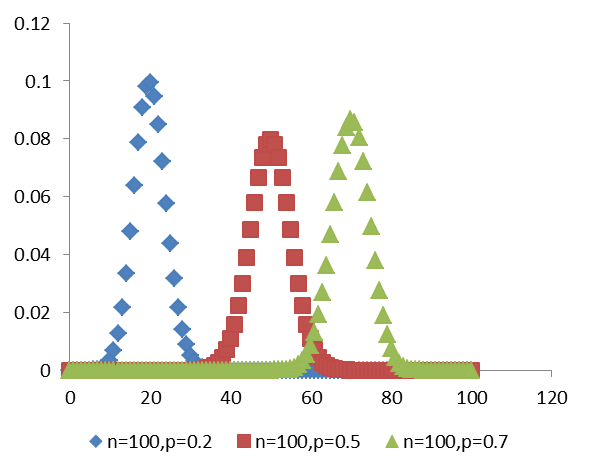
1.當p=q時圖形是對稱的
例如, ,p=q=1/2,各項的機率可寫作:
,p=q=1/2,各項的機率可寫作:


2.當p≠q時,直方圖呈偏態,p<q與p>q的偏斜方向相反。如果n很大,即使p≠q,偏態逐漸降低,最終成常態分配,二項分布的極限分布為常態分配。故當n很大時,二項分布的機率可用常態分配的機率作為近似值。何謂n很大呢?一般規定:當p<q且np≥5,或p>q且nq≥5,這時的n就被認為很大,可以用常態分配的機率作為近似值了。
如果二項分布滿足p<q,np≥5,(或p>q,np≥5)時,二項分布接近常態分配。這時,也僅僅在這時,二項分布的x變數(即成功的次數)具有如下性質:
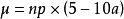

即x變數具有μ = np,的常態分配。
式中n為獨立試驗的次數,p為成功事件的機率,q=1- p。 由於n很大時二項分布逼近常態分配,其平均數,標準差是根據理論推導而來的,故用μ和σ而不用X和S表示。它們的含意是指在二項試驗中,成功的次數的平均數μ = np ,成功次數的分散程 。例如一個擲10枚硬幣的試驗,出現正面向上的平均次數為5次(μ= np=),正面向上的散布程度為√10×(1/2)×(1/2)= 1.58(次),這是根據理論的計算,而在實際試驗中,有的人可得10個正面向上,有人得9個、8個……,人數越多,正面向上的平均數越接近5,分散程度越接近1.58。
圖形特點
(1)當(n+1)p不為整數時,二項機率P{X=k}在k=[(n+1)p]時達到最大值;
(2)當(n+1)p為整數時,二項機率P{X=k}在k=(n+1)p和k=(n+1)p-1時達到最大值。
註:[x]為不超過x的最大整數。
套用條件
1.各觀察單位只能具有相互對立的一種結果,如陽性或陰性,生存或死亡等,屬於兩分類資料。
2.已知發生某一結果(陽性)的機率為π,其對立結果的機率為1-π,實際工作中要求π是從大量觀察中獲得比較穩定的數值。
3.n次試驗在相同條件下進行,且各個觀察單位的觀察結果相互獨立,即每個觀察單位的觀察結果不會影響到其他觀察單位的結果。如要求疾病無傳染性、無家族性等。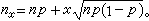 二項分布公式
二項分布公式
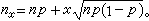 二項分布公式
二項分布公式套用實例
二項分布在心理與教育研究中,主要用於解決含有機遇性質的問題。所謂機遇問題,即指在實驗或調查中,實驗結果可能是由猜測而造成的。比如,選擇題目的回答,劃對劃錯,可能完全由猜測造成。凡此類問題,欲區分由猜測而造成的結果與真實的結果之間的界限,就要套用二項分布來解決。下面給出一個例子。
已知有正誤題10題,問答題者答對幾題才能認為他是真會,或者說答對幾題,才能認為不是出於猜測因素?
分析:此題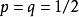 ,即猜對猜錯的機率各為0.5。
,即猜對猜錯的機率各為0.5。 ,故此二項分布接近常態分配:
,故此二項分布接近常態分配:
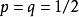


根據常態分配機率,當Z=1.645時,該點以下包含了全體的95%。如果用原分數表示,則為

它的意義是,完全憑猜測,10題中猜對8題以下的可能性為95%,猜對8、9、10題的機率只5%。因此可以推論說,答對8題以上者不是憑猜測,而是會答。但應該明確:作此結論,也仍然有犯錯誤的可能,即那些完全靠猜測的人也有5%的可能性答對8、9、10道題。
此題的機率值,還可用二項分布函式直接計算,亦得與常態分配近似的結果:
b(8 10 0.5)=10*9/2*0.58*0.52 = 45/1024
b(9 10 0.5)=10*0.59*0.51 = 10/1024
b(10 10 0.5) = 1/1024
根據機率加法,答對8題及其以上的總機率為:45/1024+10/1024+1/1024=56/1024 = 0.0547 同理,可計算8題以下的機率為 95%。(近似)