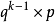介紹
伯努利試驗是一個有兩種結果的簡單試驗,它的結果是成功或失敗,黑或白,開或關,沒有中間的立場,沒有妥協的餘地。這樣的例子也特別多,例如我們觀察從一副紙牌中拿出一張牌,它或者是黑色或者是紅色;接生一個嬰兒,或者是男孩或者是女孩;我們經歷24小時的一天,或者遇到流星或者遇不到流星。在每一種情況下,很方便設計一種結果“成功”,另外一種結果為“失敗”,例如選出一張黑色牌,生出一個女兒,沒有遇到流星都可以表示為“成功”。然而,從機率的角度看,選擇紅牌、兒子、遇到流星為成功也是不會產生差異的。在這種場合下,“成功”是沒有價值取向的色彩。
單個伯努利試驗是沒有多大意義的,然而,當我們反覆進行伯努利試驗,去觀察這些試驗有多少是成功的,多少是失敗的,事情就變得有意義了,這些累計記錄包含了很多潛在的非常有用的信息。
試驗要點
重複試驗的相互獨立性
伯努利試驗是在同樣的條件下重複地、相互獨立地進行的一種隨機試驗,其中“在相同條件下”意在說明:每一次試驗的結果不會受其它實驗結果的影響,事件之間相互獨立。
獨立一詞不僅有專業定義而且還傳達了適合我們目標的含義:如果一個事件的結果不會對另一個事件的結果產生影響,那么這兩個事件是
相互獨立的。例如,史密斯生一個兒子與詹森生一個女兒是兩個獨立的事件;投一枚一角硬幣與投一枚一分硬幣的結果(正面或反面)也是相互獨立的,一枚硬幣的結果不會對另一枚硬幣的結果產生影響。但是,如果我們研究一副紙牌中的兩張牌,一次只能抽一張,並認為黑色牌為成功,於是在抽完第一張紙牌後再抽第二張紙牌時,獨立性就喪失了,因為第一張牌的結果將直接影響第二次抽取的結果。
多次試驗
判斷某種試驗是否為
伯努利試驗的關鍵是:首先,必須是重複的試驗,即多次試驗,而非一次試驗;其次,每次試驗的結果同其他各次試驗的結果無關,即事件發生的機率沒有相互之間的
影響。
伯努利試驗
在機率論中,把在同樣條件下重複進行試驗的數學模型稱為獨立試驗序列概型,進行n次試驗,若任何一次試驗中各結果發生的可能性都不受其它次試驗結果發生情況的影響,則稱這n次試驗是相互獨立的。特別的,當每次試驗只有兩個可能結果時,稱為n重伯努利試驗。
典例
(1)連續的n次射擊;
(2)連續的擲n次硬幣。
相關定理
設在一次試驗中,事件A發生的機率為p(0<p<1),則在n重伯努利試驗中,事件A恰好發生 k 次的機率為:
。
推論
設在一次試驗中,事件A首次發生的機率為p(0<p<1),則在伯努利試驗序列中,事件A在第 k 次試驗中才首次發生的機率為
。
特殊情形
二項分布
一般地,在n次獨立重複試驗中,ξ表示事件A發生的次數。如果事件A發生的
機率是p,則不發生的機率 q=1-p,n次獨立重複試驗中,事件A發生k次的機率是:P(ξ=k)=
(k=0,1,2,3…n),那么就說ξ服從參數p的
二項分布,其中p稱為成功機率。記作:ξ~B(n,p)。
(1)二項分布ξ的期望:Eξ=np;
(2)二項分布ξ的方差:Dξ=npq。
幾何分布
在第
n次伯努利試驗中,ξ表示是事件A第一次成功的試驗的第次,詳細的說是:前ξ-1次皆失敗,第ξ次成功。如果事件A發生的機率是p,則不發生的機率q=1-p,n次獨立重複試驗中,第k次試驗是事件A的第一次成功的機率是:P(ξ=k)=
(k=0,1,2,3…n),那么就說ξ 服從參數p的
幾何分布,其中p稱為成功機率。