基本介紹
- 中文名:幾何分布
- 外文名:Geometric distribution
- 表達式:X ~ GE(p)
- 套用學科:數學以及相關領域
- 適用領域範圍:自然數學,套用數學
- 適用領域範圍:高等數學,機率論
定義
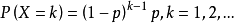
分類
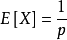
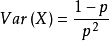

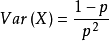
參數p的幾何分布

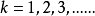

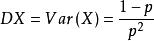
幾何分布的推廣
推廣1
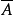



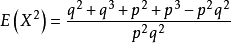

推廣2
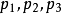



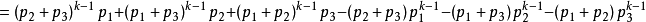
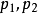


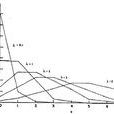
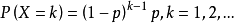
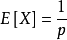
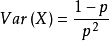

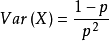

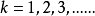

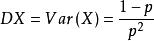
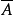



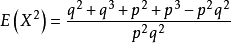

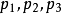



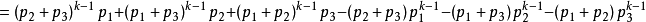
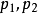


幾何分布(Geometric distribution)是離散型機率分布。其中一種定義為:在n次伯努利試驗中,試驗k次才得到第一次成功的機率。詳細地說,是:前k-1次皆失敗,第k次成功...
帕斯卡分布,負二項分布的正整數形式,描述第n次成功發生在第x次的機率,是統計學上一種離散機率分布,常用於描述生物群聚性,醫學上用來描述傳染性或非獨立性疾病的...
格點分布亦稱算術分布,是指一類離散型機率分布。稱隨機變數服從算術分布,如果其一切可能值構成(有限或無限)等差數列,即其一切可能值可以表示為a±md(m=0,1,2,...
所謂電流分布,是指理想的假定電極反應過程不存在著極化的條件下,電流在陰極表面各部位上的分布。換句話說,研究初次電流分布,就等於把電化學因素及其他方面的干擾排除...
負指數分布又稱指數分布。泊松事件流的等待時間(相繼兩次出現之間的間隔)服從指數分布。用於描述非老化性元件的壽命(元件不老化,僅由於突然故障而毀壞)。常假定排隊...
離散分布( discrete distribution)如果隨機變數X的所有可能的取值是有限或者可列無窮多個,那么它分布函式的值域是離散的,對應的分布為離散分布。常用的離散分布有二項...
《動態幾何與數的圖模(圖碼技術)》一書包括了一維運動傳遞圖模與態演繹分析;一、二交織運動刻畫基本型圖模;2nA(α)-1B型圖模及態型分析;數的圖模;整數模...
伯努利試驗幾何分布 在第n次伯努利試驗中,ξ表示是事件A第一次成功的試驗的第次,詳細的說是:前ξ-1次皆失敗,第ξ次成功。如果事件A發生的機率是p,則不發生的...
1.理解導數和微分的概念,理解導數與微分的關係,理解導數的幾何意義,會求平面曲線的切線方程和法線方程,了解導數的物理意義,會用導數描述一些物理量,理解函式的可導...
