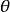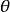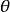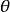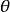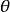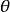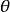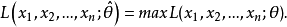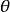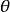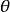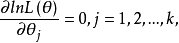極大似然估計方法（Maximum Likelihood Estimate，MLE）也稱為最大概似估計或最大似然估計，是求估計的另一種方法，最大概似是1821年首先由德國數學家高斯（C. F. Gauss）提出，但是這個方法通常被歸功於英國的統計學家。羅納德·費希爾（R. A. Fisher）
基本介紹
- 中文名：極大似然估計
- 外文名：（Maximum Likelihood Estimate)
- 又稱：最大概似估計或最大似然估計
- 屬於：求估計的一種方法
- 學科：數學
- 簡稱：MLE
- 提出者：高斯（C. F. Gauss）
研究歷史,原理,求解步驟,極大似然估計,
研究歷史
極大似然估計方法是求估計的另一種方法,1821年首先由德國數學家C. F. Gauss（高斯）提出，但是這個方法通常被歸功於英國的統計學家R. A. Fisher（羅納德·費希爾），他在1922年的論文On the mathematical foundations of theoretical statistics, reprinted in Contributions to Mathematical Statistics (by R. A. Fisher), 1950, J. Wiley & Sons, New York 中再次提出了這個思想，並且首先探討了這種方法的一些性質.極大似然估計這一名稱也是費希爾給的。這是一種目前仍然得到廣泛套用的方法。
原理
它是建立在極大似然原理的基礎上的一個統計方法，極大似然原理的直觀想法是，一個隨機試驗如有若干個可能的結果A，B，C，... ，若在一次試驗中，結果A出現了，那么可以認為實驗條件對A的出現有利，也即出現的機率P(A)較大。極大似然原理的直觀想法我們用下面例子說明。設甲箱中有99個白球，1個黑球；乙箱中有1個白球．99個黑球。現隨機取出一箱，再從抽取的一箱中隨機取出一球，結果是黑球，這一黑球從乙箱抽取的機率比從甲箱抽取的機率大得多，這時我們自然更多地相信這個黑球是取自乙箱的。一般說來，事件A發生的機率與某一未知參數
有關， 取值不同，則事件A發生的機率
也不同，當我們在一次試驗中事件A發生了，則認為此時的 值應是t的一切可能取值中使 達到最大的那一個，極大似然估計法就是要選取這樣的t值作為參數t的估計值，使所選取的樣本在被選的總體中出現的可能性為最大。
極大似然估計，只是一種機率論在統計學的套用，它是參數估計的方法之一。說的是已知某個隨機樣本滿足某種機率分布，但是其中具體的參數不清楚，參數估計就是通過若干次試驗，觀察其結果，利用結果推出參數的大概值。極大似然估計是建立在這樣的思想上：已知某個參數能使這個樣本出現的機率最大，我們當然不會再去選擇其他小機率的樣本，所以乾脆就把這個參數作為估計的真實值。
當然極大似然估計只是一種粗略的數學期望，要知道它的誤差大小還要做區間估計。
求解步驟
1.求極大似然函式估計值的一般步驟：
（1） 寫出似然函式；
（2） 對似然函式取對數，並整理；
（3） 求導數 ；
（4） 解似然方程 。
2.利用高等數學中求多元函式的極值的方法，有以下極大似然估計法的具體做法：
(1)根據總體的分布，建立似然函式 
;
(2) 當 L 關於 
可微時，(由微積分求極值的原理）可由方程組
定出
，稱以上方程組為似然方程.
因為 L 與 
有相同的極大值點，所以也可由方程組
定出 ，稱以上方程組為對數似然方程； 就是所求參數
的極大似然估計量。
極大似然估計
1.若總體X為離散型，其機率分布列為
其中 為為未知參數。設
是取自總體的樣本容量為n的樣本，則 的聯合分布律為
。又設 的一組觀測值為
，易知樣本
取到觀測值
的機率為
這一機率隨 的取值而變化，它是 的函式，稱
為樣本的似然函式。
2.若總體X為連續型，其機率密度函式為
，其中 為未知參數。設 是取自總體的樣本容量為n的簡單樣本，則 的聯合機率密度函式為
。又設 的一組觀測值為 ，則隨機點 落在點 的鄰邊（邊長分別為
的n維立方體）內的機率近似地為
。
考慮函式
極大似然估計法原理就是固定樣本觀測值 ，挑選參數 使
問題是如何把參數 的極大似然估計 求出。更多場合是利用
是 的增函式，故與 在同一點處達到最大值，於是對似然函式取對數，利用微分學知識轉化為求解對數似然方程
